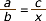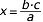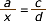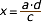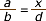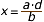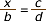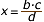PROPORCIONALITAT DIRECTA: Llegeix i memoritza

És molt important que memoritzis

Magnituds directament proporcionals

A la introducció d'aquest tema, hem vist exemples amb parelles de magnituds que tenen la propietat que si una d'elles es multiplica, o divideix, per un nombre, aleshores l'altra queda multiplicada o dividida pel mateix nombre. Les parelles de magnituds que tenen aquest comportament es diuen directament proporcionals.

Més exactament:

Exemples

Raó i proporció

En poques paraules, una raó és una fracció, és a dir, el quocient de dos nombres a i b, i una proporció és la igualtat de dues raons.

Una raó és una fracció, o quocient, de dos nombres a i b: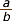

Donat que una raó és una fracció, si multipliquem o dividim els seus dos elements per un mateix nombre, k, obtindrem una raó equivalent (no oblideu això!) Convé que apreneu les formes de parlar quan ens referim a raons, formes de parlar que s'utilitzen molt en llenguatge ordinari. Així, és molt probable que hagueu sentir frases com

Observació:

Si dues magnituds són directament proporcionals, aleshores en dividir dos valors, x i y, que es corresponguin, obtindrem sempre el mateix resultat, és a dir, la raó és constant. És per això que s'anomena raó de proporcionalitat directa, o constant de proporcionalitat.

La raó de proporcionalitat directa s'obté dividint dues quantitats qualssevol que es corresponguin

Exemple
•	Si un cotxe va sempre a una velocitat de 50 Km per hora (Km/h), en posar diferents temps de moviment i les distàncies recorregudes, veiem que s'obté una raó de proporcionalitat igual a 50.
Observeu que és el mateix dir que "la raó de l'espai al temps és constant" que dir que "l'espai sempre és igual al temps invertit multiplicat per la raó de proporcionalitat" (e = 50·t, ja que 100=50·2, 150=50·3, 200=50·4, etc.). Així doncs,
Si x i y representen magnituds directament proporcionals, aleshores y = k·x, on k és la raó de proporcionalitat.

 

Una proporció és la igualtat de dues raons:

Convé que apreneu la terminologia sobre proporcions i les dues propietats bàsiques: • La proporció se sol llegir dient a és a b com c és a d. Encara que ja molt poc, també se sol veure escrita així  a:b :: c:d • Els termes a i d se solen anomenar extrems. Els termes b i c se solen anomenar mitjans • Primera propietat bàsica de les proporcions: En qualsevol proporció, el producte dels extrems coincideix amb el producte dels mitjans. Més exactament: Si aleshores a·d = b·c i  recíprocament   Aquesta propietat us permetrà saber ràpidament si 4 nombres a, b, c, d formen una proporció. Per exemple, 3, 7, 6, 14, donats en aquest ordre, formen una proporció, perquè 3·14 = 42  i  7·6 = 42.  En canvi, 3, 7, 5, 10 no formen proporció, perquè 3·10 = 30  i  7·5 = 35, que no és igual a 30. • Segona propietat bàsica de les proporcions: Si aleshores i   Com es calcula un terme d'una proporció, si es coneixen els altres tres? Normalment, els problemes de proporcionalitat solen conduir a una proporció en la que es desconeix el valor d'un dels quatre elements i es coneixen els altres tres. Aleshores, calcular l'element desconegut és fàcil, si s'utilitza la primera propietat bàsica de les proporcions. Observeu com: Si aleshores a·x = b·c. Per tant, Si aleshores a·d = c·x. Per tant, Si aleshores a·d = b·x. Per tant, Si aleshores d·x = b·c. Per tant, Exemples Si els nombres 5, 12, x, 84 formen una proporció, quant val el terme x ? La resposta és fàcil: Primer, formen la proporció; després, apliquem la primera propietat bàsica i, finalment, aïllem x. Observeu com: Obtindreu més exemples, tants com vulgueu, en la següent escena.

Regla de tres simple

Com hem dit, els problemes de proporcionalitat solen conduir a una proporció que conté un element desconegut. Per arribar a la proporció on es destaca l'element, x, desconegut, se sol utilitzar un esquema d'organització del raonament conegut amb el nom de regla de tres simple:

Regla de tres simple		Esquema
1.	S'emparellen les dades d'una magnitud amb les de l'altra: A la dreta de les dades d'una magnitud es posen les de l'altra.
2.	Al costat de la dada sense parella es posa la incògnita, x.
3.	Es formen les raons en vertical i, igualant-les, s'obté la proporció final. Quan la proporcionalitat és directa, aquestes raons es formen en els dos costats en el mateix sentit: En els dos de dalt a baix, o en els dos de baix a dalt (el motiu és clar: les dues raons coincidiran amb la raó de proporcionalitat.)

Percentatges

En poques paraules, un percentatge és una raó amb el denominador igual a 100, però en compte d'expressar-la com a fracció, s'escriu posant només el numerador a, i després, el símbol %.

Per indicar la raó , s'escriu n% i es llegeix n per cent.  Per tant, no l'oblideu, n% significa n de cada 100.

Exemples

1.	Mitjançant una regla de tres, és senzill calcular percentatges. Per exemple, per calcular el 24% de 68 €, podem raonar així:	IMPORTANT! Si us fixeu en la resolució de l'exemple, veureu que, per calcular el 24% de 68, hem acabat multiplicant el 68 pel 24 i hem dividit per 100 el resultat. Així doncs, Per calcular el n% d'una quantitat, Q, podem multiplicar Q per n i dividir per 100 el resultat.
2.	Mitjançant una regla de tres, és senzill sumar l'IVA a un preu. Per exemple, per sumar el 16% d'IVA a un preu de 85 €, podem raonar així:	IMPORTANT! Si us fixeu en la resolució de l'exemple, veureu que, per sumar l'IVA a 85€, hem acabat multiplicant el 85 per 1'16. Així doncs, Per sumar el n% a una quantitat, Q, és suficient multiplicar Q per (1+n/100).
Obtindreu més exemples en la següent escena.

Proporcionalitat geomètrica

En Geometria, la proporcionalitat juga un paper essencial, en ella es fonamenta, per exemple, tot allò que es refereix a la semblança de figures. Podeu quedar-vos amb aquesta idea: Dues figures s'anomenen semblants si una d'elles és com una ampliació fotogràfica de l'altra (en el cas dels triangles, això vol dir exactament que tenen els costats homòlegs directament proporcionals.)

Aquí, només tractarem el cas de semblança de triangles, i tampoc no ho farem de forma completa. Ja ho estudiareu en cursos posteriors. En la propera quinzena, però, tornarem a referir-nos una mica a figures semblants.

Es diu que dos triangles, APQ i ABC, estan en posició de Thales, si compleixen les següents condicions:
1.	Tenen un vèrtex comú (en la figura adjunta, A)
2.	Els costats concurrents en A estan superposats (AQ i AC,  AP i AB), o sigui, un triangle està encaixat en l'altre.
3.	Els altres dos costats són paral·lels (costats PQ i BC).
Teorema de Thales*
Dos triangles en posició de Thales tenen els costats homòlegs directament proporcionals, és a dir
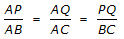* Thales fou un matemàtic grec del segle VI a.C., el primer matemàtic pròpiament dit del que es té notícia. És considerat com el primer dels set savis de la Grècia Antiga. No se sap molt sobre la seva obra, però sembla ser que fou el primer en introduir la idea de la demostració en geometria i va esbrinar l'altura d'una de les piràmides d'Egipte observant simplement l'ombra d'un pal vertical.