REPARTIMENTS DIRECTAMENT PROPORCIONALS: Assimila mètodes
En aquesta sessió, tindreu l'oportunitat d'assimilar els procediments habituals per resoldre problemes de repartiments proporcionals i d'aplicació a la resolució de problemes de mescles. A través de les escenes, cada un decidirà el nombre d'exercicis que vol llegir detalladament resolts i explicats.
| 1 | Un home va fer testament, deixant tots els seus diners en efectiu perquè fossin repartits entre els seus 3 fills, proporcionalment a les seves edats, el dia que ell morís. Quan va morir, els fills tenien 25, 22 i 21 anys, i en els comptes corrents hi havia un total de 472600 €. Quina part va rebre cada fill? |
| Resolució | ||
| Si posem |
||
x =
quantitat per al fill gran, y=
quantitat per al 2n, z =
quantitat per al petit |
||
| haurem de resoldre les proporcions següents: | ||
| Com que 25+22+21 = 68, obtenim | ||
| 2 | Tres socis, A, B i C, munten una empresa posant cada
un una part del capital necessari. B posa el doble que A i C el doble
que B. Si al final del primer any s'han de repartir els 50400 € de
beneficis, quan li tocarà a cada un, si el repartiment es fa proporcionalment
al que van aportar inicialment? Indicació: Imagina que A va posar 1 € i fes un repartiment directament proporcional a 1, ? i ? |
| Resolució | ||
| Seguint la indicació, si suposem que A va arriscar 1 € per muntar l'empresa, aleshores B va posar 2·1 = 2 €, i C va posar el doble que B, és a dir, C va posar 4 €. Aleshores, haurem de repartir 50400 € en parts proporcionals als nombres 1, 2 i 4 | ||
| Com en el problema anterior,
si posem |
||
x =
quantitat per al soci A, y=
quantitat per al soci B, z
= quantitat per al soci C |
||
| haurem de resoldre les proporcions següents: | ||
| Com que 1+2+4 = 7, obtenim | ||
|
Nota: Podeu comprovar
que si se suposa que A va aporatar una quantitat diferent de 1€,
surten els mateixos resultats. Per exemple, feu-lo suposant que A va
posar 1000 € per constituir l'empresa. |
||
En l'escena següent, teniu la possibilitat de veure més problemes
resolts, similars als anteriors.
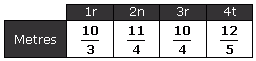
| 3 | Un edifici té 4 pisos, les altures dels quals, en metres, són les següents: | |
 |
||
| Expressa en forma de nombre decimal, i amb 2 xifres decimals, l'altura total de l'edifici. | ||
| Resolució | |||
| òbviament, l'altura de l'edifici serà
la suma de les fraccions indicades: |
|||
| Com que dues fraccions tenen igual denominador, les sumarem primer: | |||
| Així doncs | |||
| Altura total de l'edifici
= |
||
= |
= |
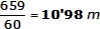 |
||
| (A la dreta us recordem la forma de convertir la fracció resultant en nombre decimal: "Es divideix el numerador pel denominador") | |||
| 4 | Reparteix 472 en parts inversament proporcionals als números 2, 5 i 7. |
| Resolució | ||
| Recordeu que repartir en parts inversament proporcionals a 2, 5 i 7 vol dir repartir en parts proporcionals als inversos 1/2, 1/5 i 1/7. Per tant, hem de resoldre les proporcions següents: |
||
| La suma de les tres fraccions 1/2, 1/5 i 1/7 val | ||
| Per tant, hem de resoldre les proporcions | ||
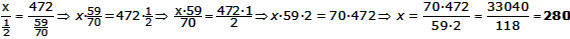 |
||
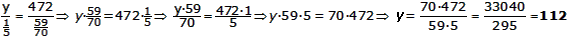 |
||
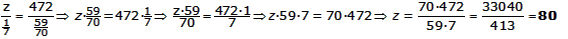 |
||
En l'escena següent, teniu la possibilitat de veure resolts més
exercicis de sumes de fraccions i repartiments inversament proporcionals.
| 5 | Mesclant vi de 8 €/litre amb vi de 1 €/litre, es volen obtenir 1400 litres de vi al preu de 3 €/litre. Quants litres de cada classe s'han de mesclar? |
| Resolució | ||
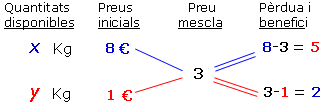
Formem l'esquema d'organització
dels càlculs a partir de les diferències entre els preus
inicials i el preu final de la mescla: |
||
 |
||
| Ara formem la proporció amb les quantitats disponibles, el benefici i la pèrdua: | ||
| Com que x+y=1400, i 2+5=7, obtenim | ||