CARÀCTER A PRIORI DE LES CIÈNCIES FORMALS:
Les ciències formals no són el resultat de cap experimentació, per això diem que són a priori. No tenim “laboratoris” de matemàtiques per a fer-hi cap mena d’experiment. No calen experiments. N’hi ha prou amb pensar. Podem fer servir un llapis i un paper per ajudar la memòria, o bé una calculadora o un ordinador per a calcular més ràpidament, però això no aporta res d’essencial: l’únic essencial és fer servir el raonament.
Les matemàtiques o la lògica no ens parlen de la realitat sinó de la nostra manera de veure i pensar la realitat. Per exemple:
Així un punt, una recta, un triangle o una arrel quadrada no són res? Quina mena de “cosa” són? Què creus que són?
La lògica i la matemàtica són eines que l'home ha desenvolupat per intentar comprendre la realitat, però no hem de confondre aquestes eines amb la realitat mateixa.
Ja que no parlen de la realitat, no són ni certes ni falses, sinó coherents o incoherents. Ser incoherents significa ser contradictòries, i en aquest cas les rebutjarem. Dos enunciats són contradictoris quan afirmen i neguen el mateix al mateix temps. Si uns mateixos principis matemàtics o lògics ens permeten afirmar “A” per una banda, i “no A” per una altra banda, direm que són contradictoris i caldrà que els modifiquem o suprimim.
ELEMENTS DE LES CIÈNCIES FORMALS:
Les ciències formals són estrictament demostratives. Si recordem el que explicàvem sobre la demostració, dèiem que si tot s’hagués de demostrar res no es podria demostrar. Les primeres premisses de qualsevol demostració (els principis) han de provenir o bé de l’experiència o bé de la intuïció. Les ciències formals són a priori, és a dir, fonamenten els seus principis en la intuïció. Aquests principis són les definicions i els axiomes i postulats.
DEFINICIONS:
Les matemàtiques i la lògica han de començar per definir els seus objectes i funcions. Per exemple: en lògica definim què és una proposició, què és una condicional, un valor veritatiu, etc. En matemàtiques comencem per definir els nombres, les funcions, els punts, les rectes, els vectors, etc.
Cal diferenciar les definicions matemàtiques i lògiques (a priori) de les definicions empíriques (a posteriori) que utilitzen les altres ciències:
-Les definicions empíriques intenten representar què és el que hi ha al nostre voltant (lleons, homes, taules...) o les seves característiques (blau, sòlid, mamífer, volador...)
-Les definicions formals són creacions humanes o invencions (connectiva, nombre, punt, recta...), en lloc de ser representacions dels objectes, però estan pensades de tal manera que poden servir per entendre millor tot allò que ens envolta. Per exemple, si dic que la pissarra és rectangular no significa que la pissarra es correspongui exactament a la definició de “rectangle”, però amb aquesta idea podré calcular-ne la superfície o bé calcular quantes me’n cabran en un determinat lloc.
PRINCIPIS AXIOMÀTICS I POSTULATS:
Els principis axiomàtics, o simplement axiomes, i els postulats són proposicions indemostrables, però evidents, és a dir, que veiem clares gràcies a la intuïció.
Hi ha un principi del qual no podem prescindir en cap sistema matemàtic o lògic: el principi de contradicció, que podem formular de la següent manera:
“És impossible afirmar i negar el mateix al mateix temps i des del mateix punt de vista”.
Aquest principi no es pot demostrar, però és el fonament de tota demostració posterior. Si algú ens diu que no hi està d’acord, l’únic que podem fer és deixar d’intentar raonar amb ell, perquè quan afirmi x, estarà admetent que també podria haver negat x pels mateixos motius que li han servit per afirmar-ho, és a dir, es contradirà sense que això li importi.
Altres exemples d’axiomes els trobareu al text d'Asimov "El electrón zurdo y otros ensayos científicos".
Els postulats són més o menys el mateix que els axiomes. També són indemostrables i es coneixen intuïtivament. La diferència és que els axiomes solen ser més generals i els postulats més específics d’una disciplina determinada. Però hi ha autors que utilitzen indistintament els dos termes.
TEOREMES:
A partir d'aquests tres elements (definicions, axiomes i postulats), i utilitzant únicament la deducció, s'obtenen conclusions que anomenem teoremes. Els teoremes són les lleis matemàtiques i lògiques que solem utilitzar per als càlculs més complexos. La característica bàsica d’un teorema és que es pot demostrar partint de les definicions i els axiomes i postulats.
Tipus de geometria |
Nombre de paral·leles |
Suma dels angles dels triangles |
Lobachevski |
∞ |
< 180º |
Euclides |
1 |
180º |
Riemann |
0 |
> 180º |
En la búsqueda de un axioma que reemplace al de las paralelas de Euclides, podemos seguir dos caminos opuestos:
Podemos decir que, en un plano, por un punto exterior a una recta no pasa ninguna paralela (Euclides había dicho que pasaba exactamente una).
Podemos decir que pasa más de una paralela (se demuestra luego que si hay más de una paralela, entonces habrá un número infinito de paralelas).
La primera de estas posibilidades que se apartan de Euclides fue explorada por el matemático ruso Nikolai Lobachevski, la segunda por el matemático alemán Georg Friedrich Riemann.
Examinemos más minuciosamente las dos geometrías no euclidianas. En la geometría de Lobachevski, llamada en la jerga técnica geometría hiperbólica, hay un número infinito de paralelas. En la geometría de Riemann, llamada geometría elíptica, no hay paralelas. ¿Cómo es una geometría en la que no hay paralelas? Podemos comprenderlo si pensamos en un modelo que no es exactamente el de una geometría elíptica, pero es semejante a ella: el de la geometría esférica.
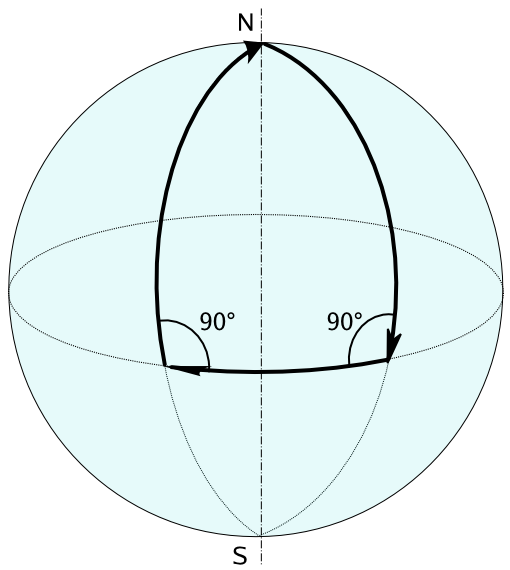
El modelo es simplemente la superficie de una esfera. Consideremos a esta superficie como análoga a un plano. Las rectas de un plano están representadas aquí por los círculos máximos de la esfera. En términos más generales, decimos que, en toda geometría no euclidiana las líneas que corresponen a las rectas de la geometría euclidiana son “líneas geodésicas”. Comparten con las rectas la propiedad de ser la distancia más corta entre dos puntos dados. En nuestro modelo, la superficie de la esfera, la distancia más corta entre dos puntos, la geodésica, es una parte de un círculo máximo. Los círculos máximos son las curvas que se obtienen intersecando la esfera con un plano que pasa por el centro de ésta. El ecuador y los meridianos terrestres son ejemplos conocidos.
En la figura anterior hemos indicado dos meridianos perpendiculares al ecuador. En la geometría euclidiana, dos líneas perpendiculares a un línea dada son paralelas, pero en la esfera estas líneas se encuentran en el Polo Norte y en el Polo Sur. En la esfera no hay líneas rectas o, más bien, casi rectas, es decir, círculos máximos, que no se corten. Aquí tenemos, pues, un modelo fácilmente concebible de una geometría en la cual no hay paralelas.
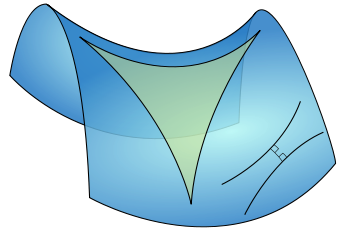
En la geometría euclidiana la suma de los ángulos de un triángulo es igual a dos ángulos rectos, o sea, 180º. En la geometría hiperbólica de Lobachevski, la suma de los ángulos de un triángulo es menor que 180º. En la geometría elíptica de Riemann, la suma es mayor que 180º.
En la geometría elíptica es fácil comprender la diferencia con respecto a los 180º con ayuda de nuestro modelo, la superficie de una esfera. Consideremos el triángulo NAB de la figura anterior: está formado por segmentos de dos meridianos y el ecuador. Los dos ángulos del ecuador tienen 90º, de modo que ya tenemos un total de 180º. Si sumamos el ángulo del Polo Norte la suma será mayor que 180. Si trasladamos los meridianos hasta que se corten en ángulo recto, todos los ángulos del triángulo serán rectos y su suma será igual a 270º.
RUDOLF CARNAP, Fundamentación lógica de la física.
En aquesta imatge podem veure un model que permet imaginar la geometria hiperbòlica de Lobachevski