UNITAT DIDÀCTICA
ÀREES DE FIGURES PLANES
German Arbiol Oliver
UNITAT DIDÀCTICA: ÀREES DE FIGURES PLANES
NIVELL EDUCATIU: 2n d’ESO
TIPOLOGIA: Es tracta d’una unitat d’assoliment de conceptes de geometria plana treballats a Primària amb aprofundiment als conceptes d’àrees del cercle i del sector circular.
CONTINGUTS
1 Magnituds i mesures.
PROCEDIMENTS
Emprar els algorísmes de càlcul de les figures planes:
1 Algorisme de càlcul de mesures de longituds.
VALOR ACTITUDS I NORMES
OBJECTIUS
Identificar figures planes, deduir i utilitzar algorismes de càlcul d’àrees.
ORIENTACIONS METODOLÒGIQUES
La unitat es planteja com un treball individual consistent en treballar unes fitxes tot treballant amb el CABRI II, amb les orientacions i suggeriments del/de la professor/a, amb un replantejament dels resultats consistent en una posta en comú del grup-classe.
FITXES DE TREBALL
FITXA 1: Mesurar longituds i superfícies.
Mesura de longituds.
Sovint necessitem mesurar distàncies: quan hi ha entre dues poblacions, quan mesura la nostra taula, les mides de la nostra habitació...
Per fer-ho utilitzem una longitud fixa: 1metre, i comptem quantes vegades aquesta longitud podem encabir-la en allò que volem mesurar.
Segons la longitud, amb el metre no en tenim prou i necessitem múltiples del metre; quilòmetres,...., o bé en tenim massa i utilitzem submúltiples: centímetres, mil·límetres,...
Activitat
Obre el fitxer mesurar.htm tot movent el punt B pots veure com es mesura el segment AB utilitzant la unitat que tens a la dreta que representa un metre:
Quan mesura de llarg la taula de l’ordinador ?: ________________.
I cabria una altra taula ?:___________.
Mesura de superfícies.
Ara volem saber quan mesura la sala d’ordinadors Per això hem de saber mesurar superfícies.
Mesurar superfícies consisteix en comptar quantes vegades un quadrat d’un metre de llarg per un d’ample ( 1 m2) podem encabir-lo és la superfície que volem mesurar.
Recorda que la mesura d’una superfície s’anomena Àrea.
Activitat.
Obre el fitxer mesurar.htm i movent els punts D i E obté diferents figures, comprova que l’àrea d’aquestes figures coincideix amb el nombre de quadrats que hi caben dintre. (El quadrat de la dreta representa 1 m2).
Tot treballant amb aquest fitxer i observant el nombre de quadrats que hi ha a l’ample i al llarg omple la següent taula:
|
Àrea |
Quadrats al llarg |
Quadrats a l’ample |
|
6 |
2 |
|
|
6 |
|
2 |
|
9 |
|
|
|
12 |
|
|
|
12 |
|
|
|
15 |
|
|
|
15 |
|
|
FITXA 2: Àrea d’un rectangle.
Suposo que et preguntaràs si cal portar el metre quadrat a sobre per mesurar superfícies, evidentment: no!!.
La taula que has omplert en la fitxa 1 t’obre la solució per calcular d’una forma més còmoda superfícies, més concretament la del rectangle.
![]() ( Recorda que un rectangle és una figura plana que té quatre costat dos a dos paral·lels i iguals i els quatre angles rectes).
( Recorda que un rectangle és una figura plana que té quatre costat dos a dos paral·lels i iguals i els quatre angles rectes).
Has observat que el producte de les dues darreres columnes et dóna l’àrea ?. Així doncs només cal calcular les longituds al llarg i al ample del rectangle per, fent el producte, tens l’àrea del rectangle.
Activitats.
1 Obre Arectangle.htm i movent els punt D i E comprova com la mesura dels quadrats al llarg – la base del rectangle – per el nombre de quadrats al ample - alçada del rectangle – ens dóna l’àrea del rectangle:
Arectangle=base x altura
2 Amb l’ajuda d’una cinta métrica mesura l’àrea de la sala d’ordinadors. m2
i del pati interior de l’Institut: m2
(Quadrat: figura plana de quatre costats iguals i quatre angles iguals)

Aquadrat= .
FITXA 3: Àrea d’un paral·lelogram.
La següent figura que anem a treballar és la d’un paral·lelogram.

(Paral·lelogram: figura plana de quatre costats dos a dos paral·lels i iguals.)
Per calcular l’àrea d’un paral·lelogram només cal veure amb la figura Aparallelogram.htm que:
Gràficament: després de definir el paral·lelogram movent el punt X, es transforma en el rectangle de baix traslladant el triangle de l’esquerra a la dreta com indica la fletxa.
Analíticament: també pots comprovar que totes dues figures tenen la mateixa àrea. Així doncs podem deduir que:
Aparal·lelogram=b · h
Activitats:
1 Mou el punt X i tot observant les mides del paral·lelogram, quina és l’altura de tots els paral·lelograms: cm. Així deduïm que en aquest cas l’àrea del paral·lelogram depèn només de la .
2 Ara cal que comprovis la fórmula de l’àrea d’un paral·lelogram. Com l’altura sempre val el mateix i el fitxer del Cabri ens dóna l’àrea, amb l’ajuda d’una calculadora comprova que altura = àrea/ base. Movent el punt X a la figura del Cabri anota les mesures de la següent taula i comprova-ho:
|
Àrea del paral·lelogram |
Longitud de la base |
Altura= àrea/ base |
|
20,79 cm |
|
|
|
|
9 cm |
|
|
19,30 cm |
|
|
|
|
7,14 cm |
|
|
16,05 cm |
|
|
3 Dibuixa a sota un paral·lelogram i calcula la seva àrea (necessitaràs un regle i…):
FITXA 4: Àrea d’un triangle.
![]()
Passem al triangle: figura plana de tres costats.
Ja saps que és la figura plana més senzilla que ens podem trobar, però la més segura, és per això que els arquitectes l’utilitzen en les seves construccions: ponts, teulades, etc...
La figura Atriangle.htm t’ajudarà a veure com deduir una fórmula per calcular la seva àrea.
Pots observar en aquesta figura que tant en el triangle acutangle com en l’obtusangle al moure el vèrtex A i traçant l’altura del triangle, aquest es pot descomposar en dos triangles: 1 i 3, que al doblar-los 2 i 4 m’apareix un rectangle, la qual cosa ens diu que l’àrea del triangle és la meitat de la del rectangle:
Atriangle=Aparal·lelogram/2=b·h/2
Activitats.
1 Mou el punt A i observa les àrees de cada rectangle. Com són ? .
2 Per què creus que passa això ?: .
3 Bé ara toca mesurar i calcular. Mesura l’àrea dels triangle de sota, de l’escaire que té el professor, i dels triangles que hi ha al sostre del gimnàs.
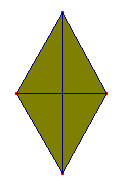 Fitxa 5: Àrea del rombe.
Fitxa 5: Àrea del rombe.
Un rombe és una figura plana de quatre costats iguals amb les diagonals perpendiculars i que es tallen en el punt mig.
Diagonal d’un polígon és el segment que uneix dos vèrtex no consecutius.
Amb la figura Arombe.htm pots veure gràficament que es pot descomposar el ronbe amb quatre triangles iguals, amb la qual cosa podem dir que l’àrea del rombe serà quatre vegades la d’un triangle.
Activitats:
1 Mou els punts A i B. Obté sis rombes diferents i, fent els càlculs adients, omple la següent taula:
|
Àrea del rombe |
Àrea del triangle |
Àrombe/Atriangle |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Així deduïm que: (A) Arombe = .
2 Ara has de calcular l’àrea d’un rombe. Reproduint els sis rombes anteriors anota les mesures de les diagonals en la taula següent i calcula l’àrea d’un triangle aplicant la fórmula obtinguda de l’àrea d’un triangle: base x altura / 2 i comprova-ho amb les resultats de la taula anterior.
|
Diagonal Major |
Diagonal menor |
D/2 |
d/2 |
Atriangle |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Deduïm que l’àrea d’un triangle és : (D/2 · d/2) /2.
3 De les conclusions de les dues taules anteriors obtenim la fórmula de l’àrea del rombe:
Àrea del Rombe = 4 Atriangle = 4 ((D/2 · d/2)/2) = (D · d) / 2
FITXA 6 : Àrea del trapezi.
 Un trapezi és una figura plamna de quatre costats amb dos costats paral·lels que s’anomenen bases.
Un trapezi és una figura plamna de quatre costats amb dos costats paral·lels que s’anomenen bases.
Utilitzaràs el fitxer Atrapezi.htm per deduir la fórmula que ens calculi l’area d’un trapezi.
Activitats
1 Mou els punt A i B per definir el trapezi. Observa, a la figura de sota, que :
a) girant el trapezi respecte la recta r.
b) tornant-lo a girar respecte la recta s.
c) traslladant-lo amb el vector v.
s’obté un paral·lelogram que té d’àrea el doble del trapezi.
Això indica que l’àrea del trapezi és la meitat de la del paral·lelogram.
Comprova-ho analíticament amb set trapezis:
|
Àrea Trapezi |
Àrea Paral·lelogram |
Àparal./Atrapezi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Calcula l’àrea del paral·lelogram . Observa que la seva base és la base major del trapezi + base menor del trapezi.:
Atrapezi =( ( B + b) · h) / 2
Fitxa 7: Àrea d’un polígon regular.
S’anomena polígon regular a aquella figura plana que té tots els costats iguals.
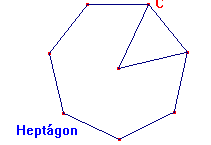
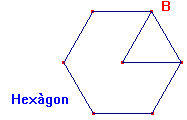
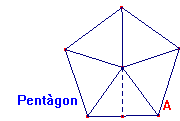
Com pots preveure el càlcul de l’àrea vindrà donat per l’àrea d’un triangle.
Activitats.
1 Obre el fitxer Apoligonregular.htm. Gràficament s’observa que el pentàgon és vegades el triangle. L’hexàgon és _ vegades el triangle, i l’heptàgon és vegades el triangle.
2 Comprova analíticament que això és compleix. Movent els punts A i B anota tres resultats per cada polígon i comprova-ho.
|
Àrea pentàgon |
Àrea triangle |
Apentàgon/Atriangle |
|
|
|
|
|
|
|
|
|
|
|
|
|
Àrea hexàgon |
Àrea triangle |
Ahexàgon/Atriangle |
|
|
|
|
|
|
|
|
|
|
|
|
3 Finalment dedueix la fórmula de l’àrea d’un polígon regular de n costats. Obre el fitxer Apoligonregular2.htm Tens un octògon l’area dl qual serà _ vegades l’àrea del triangle.
Per calcular l’àrea del triangle necessites l’altura, aquesta coincideix amb allò que en el polígon regular s’anomena apotegma.
Així dons Aoctogon = [8 x (l·a)]/2 = [ (8 · l )· a] / 2 = (perímetre x apotegma) / 2.
4 Comprova , movent el punt A en el fitxer Cabri i omplint la següent taula la fórmula que acabem de deduir:
Fòrmula : A=(pxa)/2
|
Costat |
Perímetre (p) |
Apotegma (a) |
(pxa)/2 |
Aoctogon |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FITXA 8: Àrea del cercle.
 Per calcular l’àrea d’un cercle utilitzarem dos mètodes:
Per calcular l’àrea d’un cercle utilitzarem dos mètodes:
a) Com una generalització de l’àrea d’un polígon regular de infinits costats.
b) Construint un rectangle amb la mateixa àrea.
Activitats.
1 Obre el fitxer Acercle1.htm. Considera el cercle com un polígon de infinits costats. Ara l’apotegma és el radi i el perímetre és la longitud de la circumferència que com ja saps és 2·pi·r.Així que aplicant l’area d’un polígon regular deduïm:
Acercle = (perímetre x apotegma )/2 = (2·pi·r · r)/2 = (2 · pi · r2 )/2 = pi · r2
2 Comprova la fórmula deduïda en l’activitat anterior amb cinc cassos (Recorda de moure la circumferència c per obtenir els cinc exemples)
|
Radi(r)= Apotegma(a) |
Perímetre (2pir) |
(p ·a)/2 |
pi · r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 Ara a mesurar. Quina àrea té una moneda de 5 euros ?. I el rellotge de la cuina de casa teva quina àrea té?.
FITXA 9. Àrea del sector circular.
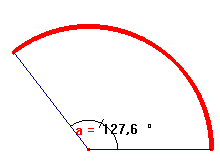
Un sector circular ve determinat pel radi amb el que es dibuixa i per l’amplitud de l’angle.
El càlcul de la seva àrea consistirà en aplicar una regla de tres, ja que el cercle es pot considerar com un sector circular de 360º.
Activitats.
1 Obre el fitxer Asector circular.htm. Interpreta que fa cada casella:
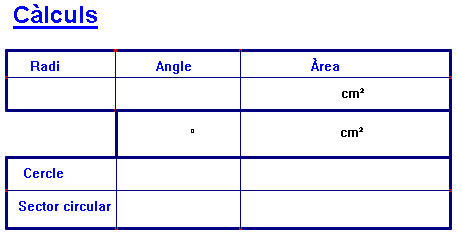
Movent el punt A aconsegueix tenir sectors circulars d’angles el donats per la taula de sota, anota els càlculs i observa la relació que hi ha amb l’àrea del cercle:
|
Angle |
Asector circular |
Acercle/Asector circ |
|
90º |
|
|
|
180º |
|
|
|
270º |
|
|
|
360º |
|
|
Com pots observar hi ha una proporció entre l’angle i la seva àrea.
Aplicant la regla de tres deduïm l’àrea d’un sector circular:
 això obtenim Asector circular=(pi · r^2 · angle)/360
això obtenim Asector circular=(pi · r^2 · angle)/360
2 Calcula l’àrea dels següents sectors circulars: