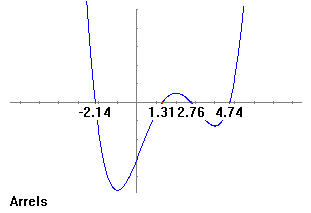
|
Aquest article explica què és funcions per a Windows, programa didàctic que va obtenir un segon premi en el "concurso de programas educativos para ordenador" organitzat pel M.E.C. l'any 1993. També són presentats uns quants exemples sobre la seva utilització. Funcions per a Windowsés un programa que representa funcions definides de forma explícita, (f(x) = sin(1/x)) o de forma numèrica mitjançant una taula de doble entrada: [(1, 2); (2,4); (3,9); (4, 16)]. El seu camp d'aplicació és en la assignatura de matemàtiques. En qualsevol domini on apareix el tema funció. Inclòs pot aplicar-se per a altres matèries en les que es treballa amb aquest concepte, com Física, Química, Economia... Permet estudiar, donada una funció, tot (casi tot), el que hi ha en les programacions oficials de l'assignatura de Matemàtiques, durant tot l'ensenyament primari, secundari i primers cursos d'ensenyament superior. El seu objectiu principal és ajudar als alumnes a aprehendre una gran majoria dels conceptes lligats amb les funcions. Així, la majoria de les opcions dels menús són referències directes lligades als mateixos, és a dir: Imatge, Antiimatge, arrels, discontinuïtats aïllades, màxims, mínims, punts d'inflexió, derivada en un punt, integral definida, integral de línia, intervals de creixement, intervals de decreixement, intervals de concavitat, intervals de convexitat, funció derivada, funció segona derivada, funció integral, punts de tall, àrea entre dues funcions. En quant a les funcions numèriques podem estudiar els distints conceptes lligats amb els temes d'interpolació i regressió. També, criem, pot facilitar l'aprenentatge d'altres conceptes relacionats amb el tema funció, no necessàriament matemàtics i, el que és més important, la seva interrelació. Això és donar-se compta de la importància del tema en altres dominis i com pot ajudar un concepte matemàtic a resoldre problemes no matemàtics. Nivells educatius: Creiem pot ésser utilitzat durant tot l'ensenyament secundari obligatori, el batxillerat i a primer curs de carreres cientifico-tècniques que precisin aquest concepte. Formes d'utilització: En primer lloc com a software educatiu tradicional, instal·lat en tots els ordinadors de l'aula i els alumnes dividits en grups, idealment dos per ordinador, es pot desenvolupar una classe dirigida pel professor o bé per un guió per a cada grup. En el manual del programa hi ha uns quants exemples d'aquestos guions o fitxes, per al professor i l'alumne. Una altra manera d'utilitzar el programa es com ajuda dels professors o alumnes per al dibuix de gràfiques. La versió Windows d'aquest programa permet fàcilment traslladar les gràfiques, mitjançant la carpeta, a altres programes com un processador de textos o programes de dibuix per afegir-hi rètols o altres indicacions. També pot ser utilitzat, amb l'ajuda d'una pantalla de vídeo o sistema de projecció de les imatges de l'ordinador (pissarra electrònica), per fer classes magistrals. Per mostrar als alumnes aquelles gràfiques i/o aquells efectes d'animació que són tan difícils d'aconseguir amb el guix a la pissarra normal. Per últim, per què no dir-ho, pot utilitzar-se en contextos no directament relacionats amb la didàctica del tema funció. Com a eina de treball, per exemple per fer un ajust de dades numèriques obtingudes mitjançant experimentació, dels quatre ajustaments que ofereix ens diu també el millor. Ho també si volguéssim seguir, i estudiar, l'evolució de les cotitzacions en borsa d'una empresa. A continuació passarem a explicar uns quants exemples de com es pot utilitzar aquest programa amb els alumnes. Exemple 1. - Estudi dels trets importants d'una funció. Representem la següent funció: f(x)=1/36(3x4-20x3+12x2+96x-110). Les arrels són els punts de tall amb l'eix d'abscisses, però el programa ens ho ensenyarà d'una manera dinàmica. El resultat final és el següent:
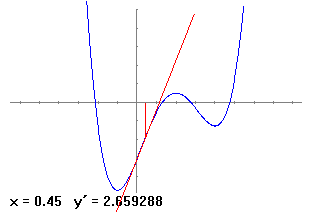
Si volem explicar el concepte de mínim local ho podem fer de varies maneres. En el dibuix de la gràfica veiem que més o menys es troba en el punt d'abscissa x = 4. Per entendre que volen dir quan diem mínim local, amb l'opció imatge en un punt calculem la imatge en el punt x = 4. Llavors calculem les imatges immediatament a la dreta i a l'esquerra del punt i veiem que són majors que la imatge en el punt x = 4. Per fer-ho, només cal prémer un botó dreta o esquerra. Podem fer una cosa semblant en el punt x = 2 per explicar que és un màxim local. Per explicar el concepte de derivada i la seva relació amb la pendent de la recta tangent ho podem explorar amb la opció amb aquest nom. Derivada en un punt. A la pantalla apareix el dibuix de la recta tangent. Prement els botons esquerra-dreta podem anar realitzant experiències i veure que on la funció és creixent, la derivada és positiva i on és decreixent la derivada és negativa.
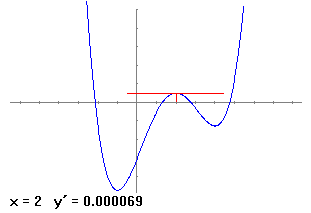
A partir d'aquí podem fer estudis una mica més sofisticats. Diem que en un màxim (o un mínim) la primera derivada s'anul·la. El programa ens ajudarà a entendre que volem dir amb això. Anem a l'opció derivada en un punt, per exemple en el punt 2 i anem veien que passa a la pantalla en els punts a la seva dreta, això ho fem prement els botons corresponents. Observem que en el mínim la recta tangent es posa horitzontal i el valor que dóna de la derivada en el punt és 0. També es va dibuixant la gràfica de la funció derivada i podem explicar perquè en els màxims la segona derivada és negativa (ja que la primera derivada és decreixent i en els mínims la segona derivada és positiva (ja que la primera derivada és creixent).
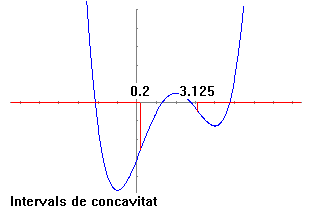
A continuació podem estudiar els intervals de concavitat i convexitat, que ens són mostrats per les corresponents opcions del menú i relacionar-les amb el signe de la segona derivada. També podem estudiar els punts d'inflexió (aquests els podem relacionar amb la primera i la segona derivada)
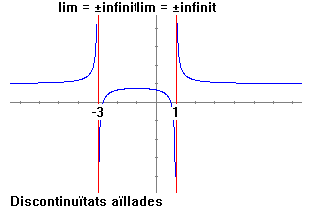
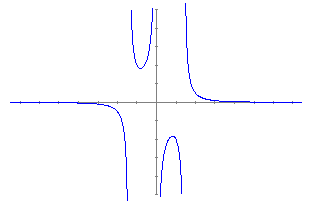
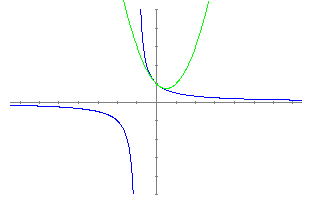
Per explicar els concepte d'asímptota vertical podem fer-ho representant una altra funció. F(x)=1/((x+3)*(x-1))+1
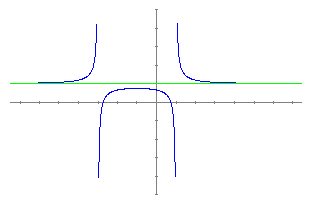
Per explicar el concepte d'asímptota horitzontal representem la mateixa funció juntament amb la recta x = 1.
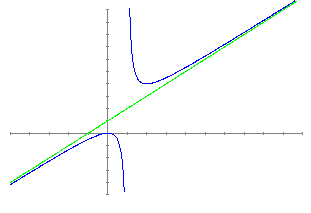
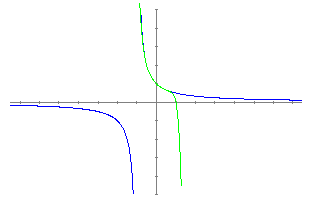
El concepte d'asímptota obliqua el podem explicar representant les dues següents funcions:
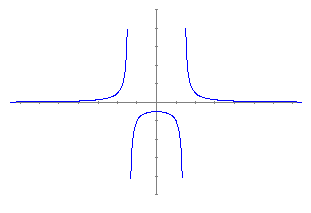
Amb l'ajuda de la opció imatge d'una funció en un punt, també, fàcilment podem explicar els concepte de simetria parell.
Representant una funció com
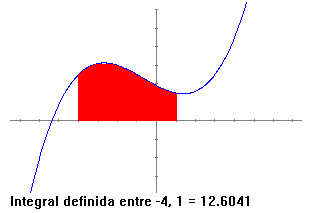
Exemple 2. - Estudi de la integral definida. Representem la següent funció: F(x)=1/20(x3+2x2-11x+38). Per veure que significa el concepte d'integral definida podem començar triant l'opció del menú amb aquest nom i calcular-la, per exemple, entre -4 i 1 i el que observem és el següent:
A partir d'aquí podem veure que passa si agafem altres intervals i a la llarga descobrirem que és l'àrea que queda per sota la corba. Agafant l'interval entre -7 i -6 veurem que passa si la funció és negativa (la integral és l'àrea negativa). També si agafem, per exemple, entre -6 i -4 veurem que passa si la funció és positiva i negativa(la integral és la suma de les àrees on la funció és positiva menys l'àrea on la funció és negativa). Utilitzant la funció sinus o cosinus podem aclarir millor aquest concepte ja que l'àrea en tot un període dóna 0. Finalment si agafem l'interval al revés, per exemple, entre 1 i -4 veiem que dóna el mateix resultat , però canviat de signe. Fins ara els exemples han estat per estudiar lo clàssic de les funcions. Els exemples següents iran a tocar unes idees més especials. També, afegim que pensem que els programes didàctics a vegades no ensenyen ni millor ni pitjor, sinó que ensenyen diferent. Aquests exemples, creiem, són un exemple clar del que volem dir. Exemple 3. - Polinomi de Taylor. Aquest exemple, que és pel nivell de COU permet veure molt fàcilment què diu, i què no diu el teorema de Taylor pel desenvolupament de funcions. Anem a veure-ho: El teorema de Taylor diu:
Sigui una funció f(x) de la qual coneixem n derivades en un punt x0. f(xo), f´(xo), f´´(xo), f´´´(xo),... , fn(xo).
El polinomi de grau n de Taylor és:
P(x)=f(xo) + f´(xo).(x-xo) + f´´(xo).(x-xo)2/2! + f´´´(xo).(x-xo)3/3! + ... + fn(xo).(x-xo)n/n! Quin és el significat?
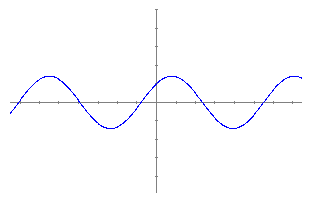
Representem la funció f(x)=sin(x)+cos(x).
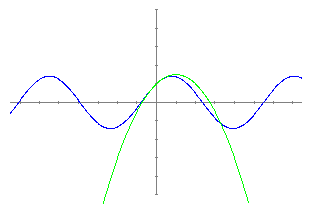
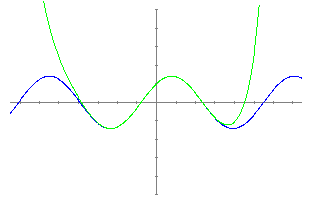
El polinomi de grau 2 és: P2(x)=1+x-x2/2 La seva representació gràfica juntament amb la funció inicial és:
El polinomi de grau 9 és: P9(x)=1+x-x2/2-x3/6+x4/24+x5/120-x6/720-x7/5040+x8/40320+x9/362880 La seva representació gràfica juntament amb la funció inicial és:
El resultat que observem és que el polinomi de Taylor és una bona aproximació de la funció inicial. A mesura que anem dibuixant polinomis de grau major l'aproximació millora. Però ens podem preguntar si això és així sempre: Representem amb el programa el polinomi de Taylor de la funció El polinomi de grau 2 és: P2(x) = 1 - x + x2
El polinomi de grau 9 és: P(x) = 1 - x + x2 - x3 + x4 - x5 + x6 - x7 + x8 - x9
Deixem al lector que tregui les seves pròpies conclusions.
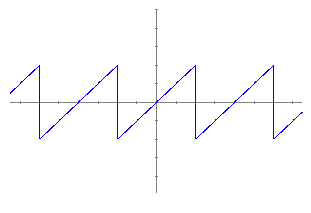
Exemple 4. - Sèries de Fourier. Aquest exemple s'escapa una mica del nivell de l'ensenyament secundari, però també demostra que algunes idees matemàtiques es poden introduir a nivells més matiners si es mostren de forma diferent. El que tracta d'explicar aquesta experiència és, que és el desenvolupament de Fourier d'una funció periòdica. En primer lloc veurem que entenem per una funció periòdica. Representarem la següent funció numèrica mitjançant interpolació lineal.
I observem la gràfica:
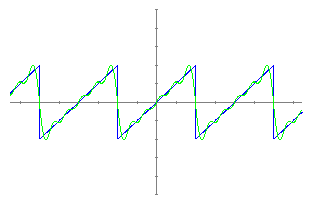
Diem què és una funció periòdica de període 4. Aquesta funció rep el nom de dent de serra. La sèrie de Fourier o desenvolupament de Fourier d'una funció f(x) es defineix per:
 On els coeficients de Fourier són: 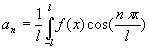 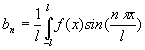 On 2l és el valor del període i n = 0,1,2,3,... El que farem a continuació és superposar els successius termes de la sèrie de Fourier damunt la funció dent de serra. Els dos primers termes: F2(x) = 1.273076 sin(px/2) -0.636292 sin(2px/2) 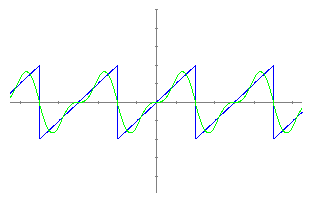 Amb cinc termes: F5(x) = 1.273076 sin(px/2) -0.636292 sin(2px/2) +0.423922 sin(3px/2)-0.317655 sin(4px/2) +0.253829 sin(5px/2)
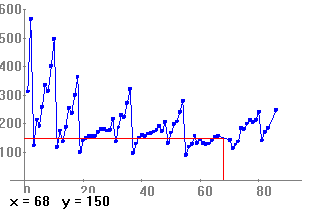
A la vista del dibuix creiem que expliquem el que volem dir. Hem dit al principi que aquest programa també es podia fer servir en camps no necessàriament de les matemàtiques, i, també, veure que el tema funció no és un tema exclusivament matemàtic. Exemple 5 . - Química: càlcul del nombre atòmic desconegut.Mendeliev quan va fer la taula periòdica dels elements tenia el problema de no disposar de tots els elements que es presenten a la natura. Quan va descobrir la taula va intuir les propietats dels elements que els faltava. Suposem que nosaltres ens trobem en una situació semblant i veiem com les matemàtiques (les funcions) ens poden ajudar en aquesta tasca. Plantegem el següent problema: La taula següent ens mostra els valors dels potencials d'ionització dels elements en funció del nombre atòmic. Calcular el potencial d'ionització del Erbi (ER) nº atòmic 68 que no apareix a la taula. nº Ato. Pot. ion. nº Ato. Pot. ion. nº Ato.Pot. ion. nº Ato. Pot. ion. nº Ato. Pot. ion.
L'únic que cal fer és representar la funció numèrica amb les parelles de dades anteriors (número atòmic, potencial d'ionització) utilitzant la interpolació lineal i cercar la imatge del valor 68. El dibuix de la gràfica amb el potencial d'ionització interpolat del Er és: (que podem comprovar en el que anomenem taula periòdica no és molt diferent del real)
Exemple 6 . -Economia: Càlcul de la quota íntegra d'una declaració de renta.Suposem que una persona ha fet la declaració de renta i ha calculat la seva base imposable, per exemple 4.800.000 ptes, que és més o menys el que ha cobrat l'any anterior i vol saber quant li toca pagar a hisenda, quota íntegra, sense desgravacions. La taula següent relaciona la quota íntegra en funció de la base imposable. És la que s'anomena escala de gravamen. Base Quota Imposable Íntegra
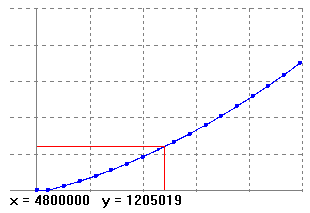
(Font: Guía practica para la cumplimentación de la declaración de renta, Hacienda Pública. Corresponent a l'exercici 1994. La declaració es va fer l'any 1995) Representem les dades anteriors utilitzant la interpolació lineal i cerquem la imatge de 4800000. La gràfica és la següent:
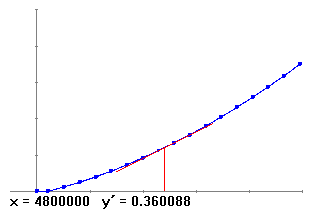
Hi ha un resultat espectacular. El que hem fet ara és utilitzar un concepte matemàtic la funció per explicar un concepte econòmic. Què és el que toca pagar a hisenda en funció del que un cobra. Però ara podrem veure com un concepte econòmic (tipus aplicable) pot ajudar-nos a entendre un concepte matemàtic (derivada en un punt). El tipus aplicable és el % que s'ha de pagar per les pessetes que passen d'un tram. Així per exemple una persona que cobri 4.800.000 pessetes ha de pagar 1.124.000 de pessetes per les primeres 4.575.000 pessetes que cobra, el tipus aplicable és el % que paga (1.205.019-1.124.000 = 81019) per les (4.800.000-4.575.000) 225.000 ptes. restants. Que és el 36%. Calculem la derivada en el punt 4.800.000.
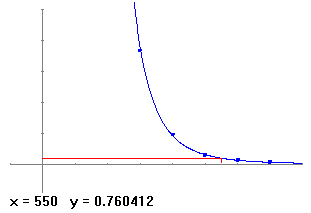
Exemple 7 . - Química: Càlcul del millor ajust, inferència d'un valor desconegut.Suposem que tenim unes dades i volem veure quin tipus de corba s'hi ajusta millor. El programa ens facilitarà aquesta tasca. Per explicar-ho, ho farem plantejant un problema: La taula següent mostra la proporció d'amoníac (%) format a diferents temperatures i pressions en una barreja inicial estequiomètrica (1N2 : 3H2) de nitrogen i oxigen
Calcular el model de regressió que s'ajusta millor amb aquestes dades. Calcular, també, el % d'amoníac format a 10 atmosferes de pressió a una temperatura de 550 C.
Per respondre a les preguntes només cal anar a representar una funció numèrica (regressió) i introduir les dues primeres columnes. Prémer al botó coeficients que ens diu quina és el tipus de corba que ajusta millor, veiem que és el potencial axb . El dibuix de la gràfica i el valor demanat, que calculem mitjançant la opció imatge és el següent:
Conclusió: Aquesta ha estat una mostra d'aplicacions didàctiques del programa "FUNCIONS per a Windows". Esperem que el lector s'hagi fet una idea de les capacitats educatives d'aquest programari i, sobretot, de donar-se compta del canvi de punt de vista que pot fer el fet d'ensenyar aquestos conceptes de manera diferent. El manual del programa presenta molts més suggeriments, exemples i fitxes didàctiques per fer-lo servir. Aquest article va ésser presentat per l'autor en les 1as jornadas de software educativo organitzades pel MEC a la seu de la UNED el juny de 1994. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i utilitzant la opció del menú imatge. Podem veure que a mesura que agafem valors més propers a 1 o -3 les imatges es disparen cap a + o - infinit. Per veure la representació de les asímptotes verticals podem utilitzar a la opció: discontinuïtats aïllades.
i la funció g(x) =x+2.
i cercant les imatges de punts aparellats com 2 i -2; 3 i -3 etc. Si fem el mateix amb la funció 
podem explicar el concepte de simetria imparell.
, en el punt 0. Que és P(x) = 1 - x + x2 - x3 + x4 - x5 + x6 - x7 +... 
