Matemàtiques - 1r BAT - Exercicis funció problemes Feliç diada de Sant Jordi per a totes i tots 1- Donades `f(x)=(x-2)/(x^2+5x+6)` i `g(x)=(x^2+4x+3)/(x^2-4)`. Trobeu l'expressió més simplificada de `f+g`, `f·g`, `f/g`, `g/f`. SOLUCIÓ: a) `f+g=(x-2)/(x^2+5x+6)+(x^2+4x+3)/(x^2-4)=(x-2)/((x+2)·(x+3))+(x^2+4x+3)/((x+2)·(x-2))=` `((x-2)·(x-2))/((x+2)·(x+3)·(x-2))+((x^2+4x+3)·(x+3))/((x+2)·(x+3)·(x-2))=` `(x^2-4)/((x+2)·(x+3)·(x-2))+(x^3+7x^2+15x+9)/((x+2)·(x+3)·(x-2))=` `(x^3+8x^2+15x+5)/(x^3+3x^2-4x-12)` b) `f·g=(x-2)/(x^2+5x+6)·(x^2+4x+3)/(x^2-4)=(x-2)/((x+2)·(x+3))·((x+3)·(x+1))/((x+2)·(x-2))=` `(x+1)/(x+2)^2` c) `f/g=(x-2)/(x^2+5x+6):(x^2+4x+3)/(x^2-4)=(x-2)/((x+2)·(x+3)):((x+3)·(x+1))/((x+2)·(x-2))=` `((x-2)·(x+2)·(x-2))/((x+2)·(x+3)·(x+3)·(x+1))=((x-2)·(x-2))/((x+3)·(x+3)·(x+1))=` `(x^2-4)/(x^3+7x^2+15x+9)` d) `g/f=(x^3+7x^2+15x+9)/(x^2-4)` 2- Donades `f(x)=x-3` i `g(x)=x/(x+1)`, calculeu, `(gof)(x)` i `(fog)(x)`. SOLUCIÓ: a) `(gof)(x)=g(f(x))=((x-3))/((x-3)+1)=(x-3)/(x-2)` b) `(fog)(x)=f(g(x))=(x/(x+1))-3=(x-3(x+1))/(x+1)=(-2x-3)/(x+1)=` 3- Donades `f(x)=(2x+1)/(x-2)` i `g(x)=(x+2)/x`, calculeu, `(gof)(x)`, `(fog)(x)`, `f^(-1)(x)` i comproveu que la inversa està ben calculada. SOLUCIÓ: a) `(gof)(x)=g(f(x))=((2x+1)/(x-2)+2)/((2x+1)/(x-2))=(((2x+1)+2(x-2))/(x-2))/((2x+1)/(x-2))=((4x-3)/(x-2))/((2x+1)/(x-2))=(4x-3)/(2x+1)` b) `(fog)(x)=f(g(x))=(2((x+2)/x)+1)/(((x+2)/x)-2)=((2x+4)/x+x/x)/((x+2)/x-(2x)/x)=((3x+4)/x)/((-x+2)/x)=(3x+4)/(-x+2)` c) `f^(-1)(x)` `y=(2x+1)/(x-2) => x=(2y+1)/(y-2)` `x·(y-2)=2y+1` `xy-2x=2y+1` `xy-2y=2x+1` `(x-2)y=2x+1` `y^(-1)=(2x+1)/(x-2)` d) `y^(-1)(y(x))=(2((2x+1)/(x-2))+1)/(((2x+1)/(x-2))-2)=((4x+2)/(x-2)+(x-2)/(x-2))/((2x+1)/(x-2)-2·(x-2)/(x-2))=((5x)/(x-2))/(5/(x-2))=(5x)/5=x` 4-Donada la següent funció definida a trossos: (Exercici 20, pàgina 225 llibre) `-2x+3` `x < -1` `f(x)=` `(x^2+1)/(x-2)` `-1 \leq x \leq 1` `sqrt(x+3)` `x > 1` a) Calcula `f(-3), f(-1), f(0), f(1)` i `f(2)`. b) Troba'n el domini. SOLUCIÓ: a) `f(-3)` està en el primer tros `=> f(-3)= -2·(-3)+3=9`. `f(-1)` està en el segon tros `=> f(-1)= ((-1)^2+1)/(-1-2)=2/(-3)=(-2)/3`. `f(2)` està en el tercer tros `=> f(2)= sqrt(2+3)=sqrt(5)`. b) Domini: El primer tros `x<-1` és un polinomi i està definit a pert tot. (-\infty, -1) és del domini. De `[-1,1]` també tots són del domini, ja que `f(x)=(x^2+1)/(x-2)` només no està definida per `x=2`, però no està `[-1,1]`. De moment, `(-\infty, -1]`, tots són del domini. En el tercer tros la funció, `f(x)=sqrt(x+3)` està definida per `x+3>0 => x>-3` com que el tercer tros va de `(1,+\infty)` tampoc cap problema. Per la qual cosa el fomini de la funció, `f(x)` sòn: Tots els reals, `R` 7- El nombre d'articles, `n`, fabricats per una empresa cada dia, en funció del temps treballat, `t`, és `n(t)=-t^2+20t`, amb una jornada laboral diària de `8` hores. El cost de producció de `n` articles és, `c(n)=5+6n`. Determina la funció, `c(t)` que dona el cost en funció de `t`. Calcula el domini d'aquesta funció. (Exercici 21, pàgina 225 llibre) SOLUCIÓ: Això és una funció composta: sí, `c(n)=5+6n` i `n(t)=-t^2+20t`. Llavors, `c(t)=c(n(t))=5+6(-t^2+20t)=-6t^2+120t+5`. Recordant el domini dels polinomis `=>`, domini de `c(t)=-6t^2+120t+5` són tots els `R` (Reals). 5-En una habitació sota teulada, que té una paret de forma triangular, hi volem posar un armari. Les mides de l'habitació són 10 metres d'amplada per 4 d'altura en la seva part més alta. Si l'armari té forma rectangular, quina han de ser les seves mides de manera que sigui el més gran possible? 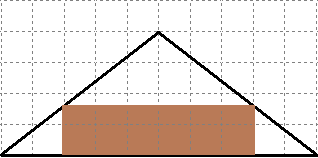SOLUCIÓ: 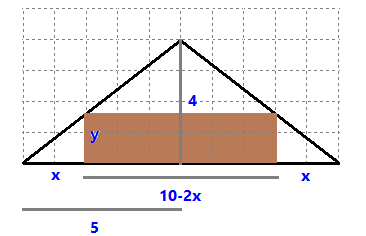Si ens hi fixem tenim dos triangles semblants per la qual cosa `y/x=4/5 => y=(4x)/5`. L'àrea de l'armari és `A=(10-2x)·y`. Si ho expressem només amb `x`, `A(x)=(10-2x)·(4x)/5=8x-8/5x^2=-8/5x^2+8x`. Qué és una funció de segon grau amb un màxim ja que el coeficient de `x^2` és negatiu, banyes avall. Per trobar el màxim només cal trobem la `x` del vèrtex. `x_v=(-b)/(2a)=(-8)/(2·((-8)/5))=(-40)/(-16)=2'5`. I la altura, `y=(4x)/5=(4·2'5)/5=2`. Les mesures són, `5` metres d'amplada per `2` d'alçada. 6-Tenim una cartolina que fa 40 cm x 60 cm. Li tallem quatre quadrats, un per cada cantonada. Dobleguem per les línies de punts i obtindrem una capsa sense tapa. La pregunta que volem contestar és quina mida de costat del quadrat hem de tallar de manera que el volum de la capsa obtinguda sigui màxim. Busca (i explica) una estratègia per trobar-ho. 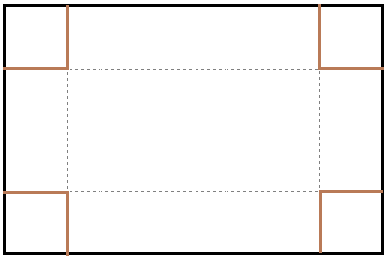SOLUCIÓ: 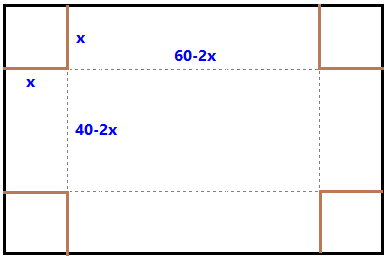Fixeu-vos que per calcular el volum ens quedarà una capsa que la seva base mesura, àrea `=(40-2x)·(20-2x)` i com l'altura serà `x`, el volum en funció de, `x`, serà `V(x)=(60-2x)·(40-2x)·x=4x^3-200x^2+2400x`. I ara el que cal és optimitzar, en aquest cas buscar el màxim, aquesta funció. Per trobar un màxim normalment el que es fa és calcular la derivada i igualar-ho a `0`. En teoria no ho sabem fer. Però aquí no va de calcular derivades, sinó de resoldre problemes. Explicaré tres maneres de fer-ho. De fet aquest problema es tret d'un llibre de tercer d'ESO (Matemàtiques 3r ESO, editorial Barcanova, pàgina 104). 1- Fent servir un full de càlcul fem una taula i mirem quin valor assoleix el màxim. 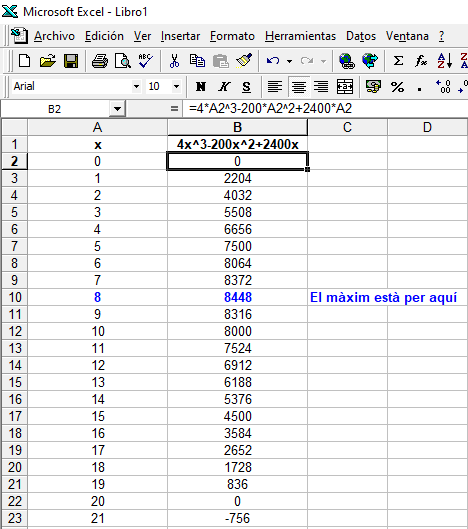2- Fent servir un programa graficador, com Funcions per a Windows i buscant el màxim. 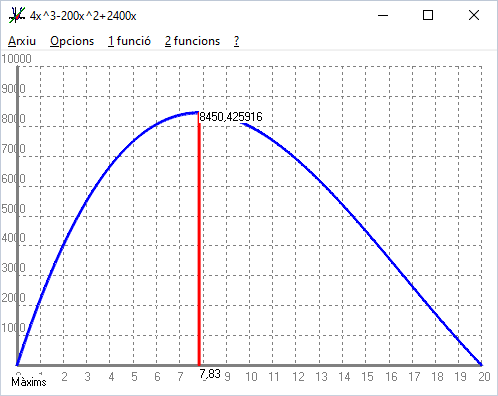3- Un dia us vaig explicar el que eren les derivades, i si mal no recordo, vaig explicar que per calcular la funció derivada d'un monomi, `f(x)=ax^2 => f'(x)=a·nx^(n-1)`. Així la derivada del nostre polinomi, `f(x)=4x^3-200x^2+2400x` serà: `f'(x)=12x^2-400x+2400`. Si no ho recordeu, cap problema, quedeu-vos amb el resultat. També recordo que la derivada tenia que veure amb el pendent de la recta tangent. Per la qual cosa en un màxim hem de trobar on la derivada val `0`. 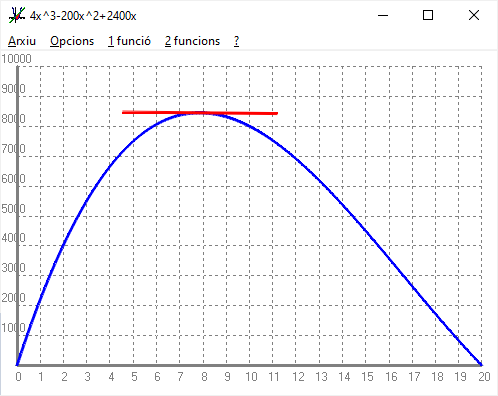En definitiva hem d'igualar al funció derivada a `0` i un dels dos resultats serà la `x` del màxim. `12x^2-400x+2400=0` les solucions aproximades són `x_1=7'85` i `x_2=25'49`. Evidentment el segon resultat no té cap sentit ja que com a màxim el tall vertical pot fer `20cm`, ja que la cartolina mesura `40cm`. O sigui si fem un tall de `7'85cm`, obtindrem una capsa sense tapa a partir de la cartolina de `60·40` de volum màxim, `f(x)=4·7'85^3-200·7'85^2+2400·7'85=8450'45 cm^3`. Aquesta última manera, pels que no hi vau ser al principi del tema, no us sonarà de res. He volgut posar aquests exercicis perquè ens en donessim compta de la gran ajuda que ens poden aportar les funcions en la resolució de problemes. Evidentment la tercera manera no és de tercer d'ESO. Oficialment ja correspondria a 2n de BAT. Per què he explicat aquesta 3a manera? Si ho voleu saber, click aquí, AFF en educación.