|
Definim `i=(1,0,0)`, `j=(0,1,0)`, `k=(0,0,1)`. Els tres vectors unitaris paral·lels als eixos. Així qualsevol vector es pot posar `(x,y,z)=x i+y j+z k`. I al revés i, per exemple, el vector, `5i+4j-3k=(5,4,-3)`. Definim el producte vectorial, `\vec(a) \times \vec(b)`, entre dos vectors `\vec(a)=(a_1,a_2,a_2)` i `\vec(b)=(b_1,b_2,b_3)` de la següent manera. El càlcul d'aquest pseudodeterminant: $$ \begin{vmatrix} i & j & k\\\ a_1 & a_2 & a_3\\\ b_1 & b_2 & b_3 \end{vmatrix} $$ Si desenvolupem el càlcul per la primera fila: $$ \begin{vmatrix}a_2 & a_3\\\ b_2 & b_3\end{vmatrix}i+\begin{vmatrix}a_3 & a_1\\\ b_3 & b_1\end{vmatrix}j+\begin{vmatrix}a_1 & a_2\\\ b_1 & b_2\end{vmatrix}k $$ $$ (\begin{vmatrix}a_2 & a_3\\\ b_2 & b_3\end{vmatrix},\begin{vmatrix}a_3 & a_1\\\ b_3 & b_1\end{vmatrix},\begin{vmatrix}a_1 & a_2\\\ b_1 & b_2\end{vmatrix}) $$ Es diu producte vectorial perquè el resultat és un vector i podem veure que es un vector perpendicular als dos vectors inicials. `a_2·b_3·a_1` `-` `a_3·b_2·a_1` `+` `a_3·b_1·a_2` `-` `a_1·b_3·a_2` `+` `a_1·b_2·a_3` `-` `a_2·b_1·a_3` `a_2·b_3·a_1` `-` `a_1·b_3·a_2` `-` `a_3·b_2·a_1` `+` `a_1·b_2·a_3` `+` `a_3·b_1·a_2` `-` `a_2·b_1·a_3=0` Això es podria haver interpretat com el càlcul del determinant: $$ \begin{vmatrix} a_1 & a_2 & a_3\\\ a_1 & a_2 & a_3\\\ b_1 & b_2 & b_3 \end{vmatrix}=0 $$ Que evidentment ha de donar `0`, ja que té dues diles iguals. Per la mateixa raó, el producte escalar amb l'altre vector , `\vec(b)`, també és `0`. El vector resultant del producte vectorial de dos vectors, `\vec(\vec(a)x\vec(b))`, és un vector perpendicular als vectors, `\vec(a)` i `\vec(b)`. Partim de la fórmula del producte escalar, `\vec(a)·\vec(b)=|\vec(a)|·|\vec(b)|·cos(alpha)` i que `cos(alpha)=sqrt(1-sin^2(alpha))` `(a_1,a_2,a_3)·(b_1,b_2,b_3)=a_1·b_1+a_2·b_2·a_3·b_3=sqrt(a_1^2+a_2^2+a_3^2)·sqrt(b_1^2+b_2^2+b_3^2)·cos(alpha)` `a_1·b_1+a_2·b_2+a_3·b_3=sqrt(a_1^2+a_2^2+a_3^2)·sqrt(b_1^2+b_2^2+b_3^2)·sqrt(1-sin^2(alpha))` Si ho elevem tot al quadrat per un costat tenim: Veiem que n'hi ha de repetits: I per l'altra: `a_1^2b_1^2+a_1^2b_2^2+a_1^2b_3^2+a_2^2b_1^2+a_2^2b_2^2+a_2^2b_3^2+a_3^2b_1^2+a_3^2b_2^2+a_3^2b_3^2-(a_1^2+a_2^2+a_3^2)·(b_1^2+b_2^2+b_3^2)sin^2(alpha)` Podem igualar els dos costats i podem treure de cadascun d'ells, `a_1^2b_1^2+a_2^2b_2^2+a_3^2b_3^2` `a_1^2b_2^2+a_1^2b_3^2+a_2^2b_1^2+a_2^2b_3^2+a_3^2b_1^2+a_3^2b_2^2-(a_1^2+a_2^2+a_3^2)·(b_1^2+b_2^2+b_3^2)sin^2(alpha)` El que hi ha a l'esquerra ho passo a la dreta i el que va amb le `sin` ho passo a l'esquerra: `a_1^2b_2^2+a_1^2b_3^2+a_2^2b_1^2+a_2^2b_3^2+a_3^2b_1^2+a_3^2b_2^2-2a_1a_2b_1b_2-2a_1a_3b_1b_3-2a_2a_3b_2b_3` (*) Ara el que farem és calcular el quadrat del mòdul del vector, producte vectorial: `(a_2·b_3-a_3·b_2)^2+(a_3·b_1-a_1·b_3)^2+(a_1·b_2-a_2·b_1)^2=` `a_2^2b_3^2-2a_2a_3b_2b_3+a_3^2b_2^2+a_3^2b_1^2-2a_1a_3b_1b_3+a_1^2b_3^2+a_1^2b_2^2-2a_1a_2b_1b_2+a_2^2b_3^2` (*) Si observem les dues expressions marcades amb (*) veiem que són iguals, la qual cosa implica que: I finalment si fem l'arrel quadrada de cada costat `|\vec(a) \times \vec(b)|=|\vec(a)|·|\vec(b)|·sin(alpha)` 1- Àrea del paral·lelogram definit pels dos vectors: 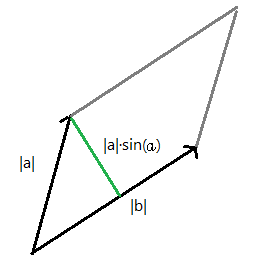 Àrea = `|\vec(a) \times \vec(b)|` 2-Àrea del triangle definit per dos vectors: 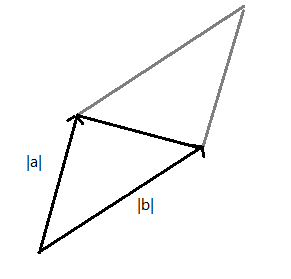 Àrea = `(|\vec(a) \times \vec(b)|)/2` 3-Distància d'un punt a una recta: Ho farem amb un exemple concret, suposem que tenim la recta. `(x,y,z)=(1,0,2)+(5,-1,3)lamda` i el punt, `(-2,4,1)`. 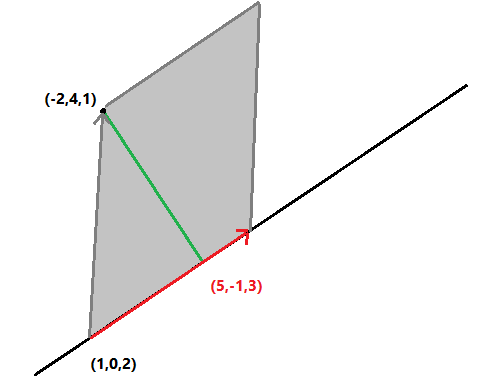 Si trobem el vector gris, `(-2,4,1)-(1,0,2)=(-3,4-1)` i calculem el producte vectorial amb el vector director de la recta, `(1,0,2)` $$ \begin{vmatrix} i & j & k\\\ -3 & 4 & -1\\\ 1 & 0 & 2 \end{vmatrix}= 8i-j-(4k-6j)=8i+5j-4k=(8,5,-4) $$ I calculem el seu mòdul `sqrt(8^2+5^2+(-4)^2)= sqrt(105) u^2` El mòdul és l'àrea del paral·lelogram gris. Per trobar l'altura, que és la distància entre el punt i la recta, només cal dividir aquesta àrea per la base, que és el mòdul del vector vermell. O sigui per calcular la distància entre un punt i una recta acabem de trobar una altra manera que és fent servir el producte vectorial. |