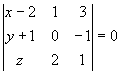|
Equacions del pla Exercici: Trobeu les equacions del pla que passa pel punt (2, -1, 0) i té com a vectors directors: (1, 0, 2); (3, -1, 1)
Equació vectorial (x, y, z) = (2, -1, 0) + m(1, 0, 2) + n(3, -1, 1)
Equacions paramètriques: x = 2 + m + 3n y = -1 - n z = 2m + n
Equació general o cartesiana x - 2 = m + 3n y + 1 = - n z = 2m + n
Ho sigui el vector (x-2, y+1, z) és combinació lineal dels dos vectros directors (1, 0, 2); (3, -1, 1) Per al qual cosa si calculem el Determinant següent ha de donar 0.
(x-2) · 0 · 1 + (y+1) · 2 · 3 + z · 1 · (-1) - (x-2) · (-1) · 2 - (y+1) ·1 · 1 - z · 0 · 3 = 0
6y + 6 - z + 2x - 4 - y - 1 = 0
2x + 5y - z + 1 = 0 Finalment l'equació general (o cartesiana) de la recta queda: 2x + 5y - z + 1 = 0 Si passem la D a l'altre costat: 2x + 5y - z = -1 I ho dividim tot per -1 -2x - 5y + z = 1 I ho posem
Aquesta última equació és diu canònica o segmentària. Només es pot calcular si tots els coeficients de les incògnites són diferents de 0. Té la propietat de que a diferència de les altres és unívoca i el número que hi ha a sota de cada incògnita és por on talla l'eix corresponent. Ho sigui -1/2 és por en talla el pla l'eix 0X (y = 0 ; z = 0). |