|
Definim el producte mixt, com el producte escalar d'un vector, `\vec(x)= (x_1,x_2,x_3)` pel resultat del producte vectorial d'altres dos, `(\vec(a) \times \vec(b))` $$ (x_1,x_2,x_3)ˇ(\begin{vmatrix}a_2 & a_3\\\ b_2 & b_3\end{vmatrix},\begin{vmatrix}a_3 & a_1\\\ b_3 & b_1\end{vmatrix},\begin{vmatrix}a_1 & a_2\\\ b_1 & b_2\end{vmatrix}) $$ Aixō es el resultat de calcular el determinant: $$ \begin{vmatrix} x_1 & x_2 & x_3\\\ a_1 & a_2 & a_3\\\ b_1 & b_2 & b_3 \end{vmatrix} $$ 1- Volum del paralˇlelepiped definit pels tres vectors: 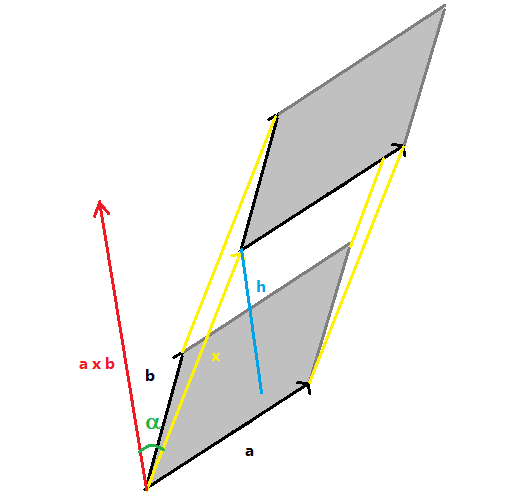 El volum és l'ārea de la base per l'altura (h). L'ārea de la base es calcula amb el mōdul del producte vectorial: L'altura es calcula multiplicant el mōdul de `\vec(x)` pel `cos(alpha)` que és l'angle que forma `\vec(x)` i la perpendicular a la base, que és la direcciķ del producte vectorial `|\vec(a) \times \vec(b)|`. Així, Que aixō és per definiciķ, `\vec(x)ˇ(\vec(a) \times \vec(b))`, que és el producte mixt tal com hem definit abans, ja que el producte escalar és el mōdul d'un vector per el mōdul de l'altre i pel `cos` de l'angle que formen. Hi posem valor absolut ja que depčn de composem els vectors ens podria donar el perpendicular per sota i l'angle seria de més de `90ē` que faria que el volum sortís negatiu. En resum, volum d'un paralˇlelepiped format per tres vectors. 1-bis- Calcula el volum d'un paralˇlelepiped definit pels vectors, `(1,0,3)` , `(-1,5,2)` i `(0,-1,1)` $$\begin{vmatrix} 1 & 0 & 3\\\ -1 & 5 & 2\\\ 0 & -1 & 1 \end{vmatrix}=5+0+3-(0+0-2)=8+2=10 u^3 $$ 2- Volum de la pirāmide de base triangular El volum d'una pirāmide és ārea de la base per altura dividit per `3`. O sigui serā igual al volum del paralˇlelepiped dividit per `3` i dividid per `2` ja que l'ārea de la base és un triangle i és l'ārea del paralˇlelogran dividida per `2`. On, `|\vec(c)ˇ(\vec(a) \times \vec(b))|` és el producte mixt dels vectors, `\vec(c)`, `\vec(a)` i `\vec(b)`. 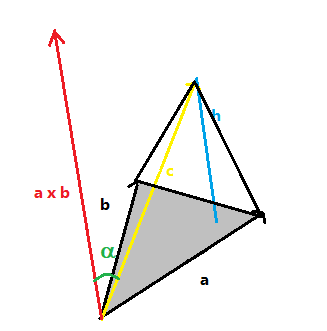 3- Cālcul de la distāncia d'un punt a un pla De la mateixa manera que el cālcul de l'ārea d'un paralˇlelogram ens ha servit per trobar la distāncia d'un punt a una recta, el volum d'un paralˇlelepiped ens pot servir per trobar la distāncia d'un punt a un pla. 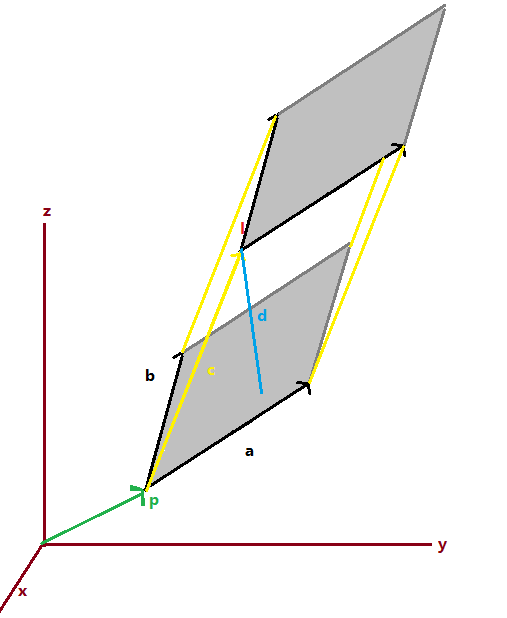 Suposem que tenim un pla amb vector de posiciō `p=(1,5,1)` i vectors directors, `(-1,5,2)` i `(0,-1,1)` i un punt `l=(2,5,4)`. Podem calcular la distāncia, `d`, dividint el volum (producte mixt) per l'ārea del paralˇlelogran (producte vectorial). `\vec(c)` és el vector que va de `p` a `l`, `(2,5,4)-(1,5,1)=(1,0,3)` $$ \frac{\begin{vmatrix}1 & 0 & 3\\\ -1 & 5 & 2\\\ 0 & -1 & 1\end{vmatrix}}{|\begin{vmatrix}i & j & k\\\ -1 & 5 & 2\\\ 0 & -1 & 1\end{vmatrix}|} $$ 4- Distāncia entre dues rectes En general la forma de calcular la distāncia entre un punt i un pla que acabem de veure no ens és gaire útil, ja l'equaciķ del pla s'acoatuma a donar-la en la versiķ general i no tenim els vectors directors. En la versiķ general ja tenim una fķrmula que ens facilita molt el cālcul. Aixō que acabem de veure ens pot servir per entendre una altra forma de calcular la distāncia entre dues rectes. 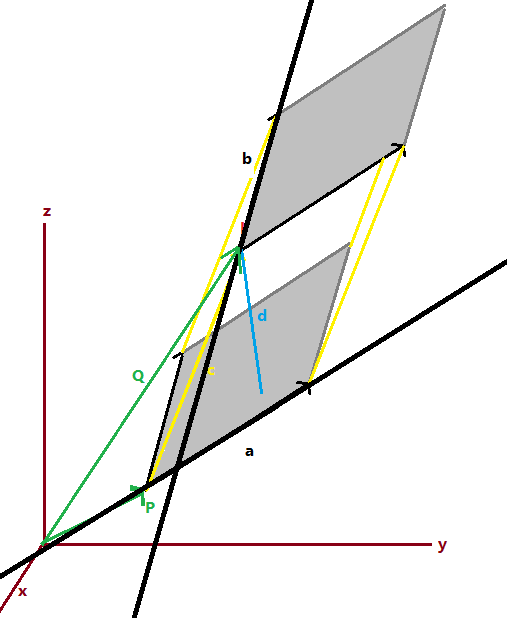 Suposem que tenim dues rectes una que passa pel punt, `P` i vector director, `\vec(a)`. I una altra recta que passa pel punt, `Q` i vector director, `\vec(b)` i volem trobar la distāncia de la primera recta a la segona. Fixeu-vos que la distāncia demanada és l'altura del paralˇlelepípede format pels vectors directors i el vector que va de `\vec(PQ)`. O sigui, per calcular la distāncia, `d`: On, `|\vec(PQ)ˇ(\vec(a) \times \vec(b))|` és el valor absolut del producte mixt de, `\vec(PQ)`, `\vec(a)` i `\vec(b)`. I `|\vec(a) \times \vec(b)|`, el mōdul del producte vectorial de, `\vec(a)` i `\vec(b)` |