1- Calcula les següents integrals:
SOLUCIÓ: a)` \int (x dx)/\sqrt{3-2x^2} = (-1)/4\int dt/\sqrt{t} dx = (-1)/4\int t^(-1/2) dx = (-1)/4t^(1/2)/(1/2) = (-1)/2\sqrt{t} = (-1)/2\sqrt{3-2x^2}+C`
b) ` \int (3x+4)/(x^2-5x+6)dx`
`(Ax-3A+Bx-2B)/(x^2-5x+6) = ((A+B)x-3A-2B)/(x^2-5x+6) = ` $$ \begin{cases}A+B=3\\ -3A-2B=4\end{cases} $$ $$ \begin{cases}A=-10\\ B=13\end{cases} $$ `(3x+4)/(x^2-5x+6) = (3x+4)/((x-2)·(x-3))=-10/(x-2)+13/(x-3) ` ` \int (3x+4)/(x^2-5x+6)dx=\int -10/(x-2)+13/(x-3) dx=-10ln(x-2)+13ln(x-3)+C` c) `\int xln^2(x) dx` Farem parts dues vegades. `\int f'g = fg -\int fg'` `f'=x => f=x^2/2` `g=ln^2(x) => g'=(2ln(x))/x` `\int xln^2(x) dx=x^2/2ln^2(x)-\int x^2/2·2ln(x)/x dx = x^2/2ln^2(x)-\int x·ln(x) dx =` *
`\int f'g = fg -\int fg'` `f'=x => f=x^2/2` `g=ln(x) => g'=1/x` `\int x·ln(x) dx = x^2/2ln(x)-\int x^2/2·1/x dx = (x^2ln(x))/2-\int x/2 dx= (x^2ln(x))/2-x^2/4` * `= (x^2ln^2(x))/2-\int x·ln(x) dx =(x^2ln^2(x))/2-[(x^2ln(x))/2-x^2/4]=(x^2ln^2(x))/2-(x^2ln(x))/2+x^2/4+C` 2- Troba l'ŕrea compresa entre les funcions `f(x) = x^2` i `g(x) = x^3` a l'interval `[0; 2]`. SOLUCIÓ: Primer cal trobar els punts de tall entre les dues funcions,
x_2=1` Per la qual cosa calcularem el valor absolut de les integrals definides entre `0` i `1` i `1` i `2` de la diferčncia entre les dues funcions. `|\int_0^1 (x^3-x^2) dx|+ |\int_1^2 (x^3-x^2) dx|=|[x^4/4-x^3/3]_0^1| + |[x^4/4-x^3/3]_1^2|=` `|(1/4-1/3)-(0/4-0/3)|+|(2^4/4-2^3/3)-(1/4-1/3)|=|1/4-1/3|+|(16/4-8/3)-(1/4-1/3)|=` `|3/12-4/12| + |16/4-8/3-1/4+1/3|= |-1/4|+|48/12-32/12-3/12+4/12|=` `1/4+|17/12|=3/12+17/12=18/12=1'5u^2` 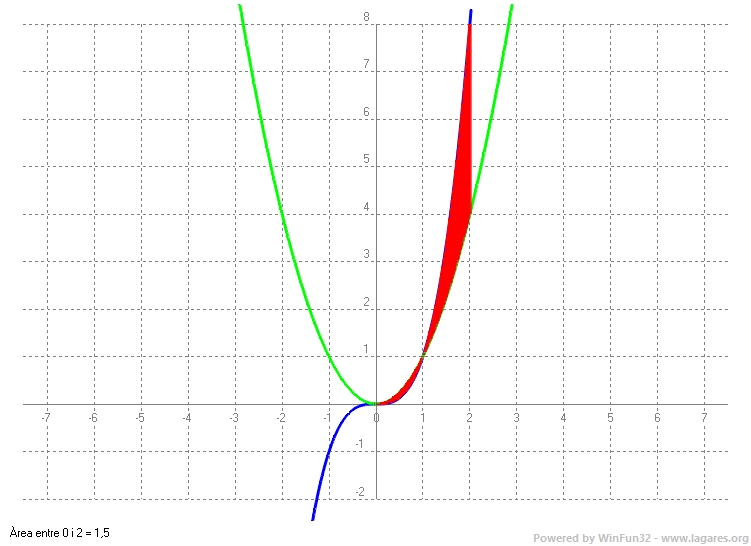 3- Calcula `p (p > 0)` per tal que la regió determinada per la grŕfica de `f(x) = xe^(3x)`, l'eix `OX` i les rectes verticals `x = 0` i ` x = p` sigui `1/9 u^2`. SOLUCIÓ:
`\int xe^(3x) dx` `\int f'g = fg -\int fg'` `f'=e^(3x) => f=e^(3x)/3` `g=x => g'=1` `\int xe^(3x) dx = xe^(3x)/3 - \int e^(3x)/3·1 dx = (xe^(3x))/3 - \int e^(3x)/3 dx= (xe^(3x))/3 - e^(3x)/9= e^(3x)/9(3x-1)` `\int_0^p xe^(3x) dx = 1/9[e^(3x)(3x-1)]_0^p = 1/9[e^(3p)(3p-1)-e^(3·0)(3·0-1)] = 1/9` `[e^(3p)(3p-1)-e^(3·0)(3·0-1)] = e^(3p)(3p-1)+ 1 = 1` `e^(3p)(3p-1) = 0 => 3p-1=0 => p=1/3` 4- Troba el volum del cos de revolució que s'obté al fer girar sobre l'eix `OX` la part positiva de la funció `f(x) = -x^2 + x + 2`. NOTA: Per trobar el volum de revolució d'una funció `f(x)` entre `x=a` i `x=b` cal calcular la integral definida `\int_a^b \pi f^2(x) dx` SOLUCIÓ: Per trobar la part positiva de la funció i tenint en compte que es tracta d'una funció de segon grau amb les branques cap avall, ja que el quoeficient de `x^2` és negatiu, `2`, cal trobar els punts de tall amb l'eix de les `x`.
`x=(-1\pmsqrt(1^2 - 4·(-1)·2))/(2·(-1))=(-1\pmsqrt(9))/(-2) = (-1\pm3)/(-2) => x_1= -1` i `x_2=2` Per la qual cosa per trobar el volum de revolució cal calcular: `\int_-1^2 \pi (-x^2+x+2)^2 dx=\int_-1^2 \pi (x^4-2x^3-3x^2+4x+4) dx =` `\pi[x^5/5-(2x^4)/4-(3x^3)/3+(4x^2)/2+4x]_-1^2 = \pi[x^5/5-x^4/2-x^3+2x^2+4x]_-1^2=` `\pi[(2^5/5-2^4/2-2^3+2·2^2+4·2)-((-1)^5/5-(-1)^4/2-(-1)^3+2(-1)^2+4·(-1))]=` `\pi[(32/5-8-8+8+8)-((-1)/5-1/2+1+2-4)]=` `\pi[32/5+1/5+1/2+1]= \pi[64/10+2/10+5/10+10/10]=81/10\pi` `u^3` |