4- Calcula les integrals següents:

a) `\int_-1 ^1 (-x)/(x^2+1) dx`



b) `\int_0 ^2 (2-3x)^5 dx`



c) `\int_2^4 3/(1-x) dx`



d) `\int_0 ^1 x/(1+x^4) dx`


    SOLUCIÓ:

      a) `\int (-xdx)/(x^2+1)=\int (-dt)/(2t)=-1/2ln t=-1/2ln(x^2+1) `

      `x^2+1=t => 2xdx=dt => xdx=dt/2`

      `\int_-1 ^1 (-x)/(x^2+1) dx=[-1/2ln(x^2+1)]_-1^1=-1/2[ln(1^2+1)-ln(1^2+1)]=-1/2[ln(2)-ln(2)]=0`

      `-1/2ln(4/2)=-1/2ln(2)=ln\sqrt{1/2}`




      b) `\int (2-3x)^5 dx=\int t^5 (-dt)/3=-1/3\int t^5 dt=-1/3t^6/6=(-t^6)/18=(-(2-3x)^6)/18`

      `(2-3x)=t => -3dx=dt => dx=-dt/3`

      `\int_0 ^2 (2-3x)^5 dx=[(-(2-3x)^6)/18]_0^2=(-(2-6)^6)/18-(-(2-0)^6)/18=-(-4)^6/18+2^6/18 = -224`




      c) `\int_2^4 3/(1-x) dx=[-3ln|1-x|]_2^4=-3[ln(3)-ln(1)]=-3ln(3)`

      Hi posem valor absolut, `ln|1-x|`, si no, no tindria sentit, ja que hi haurien logaritmes de nombres negatius.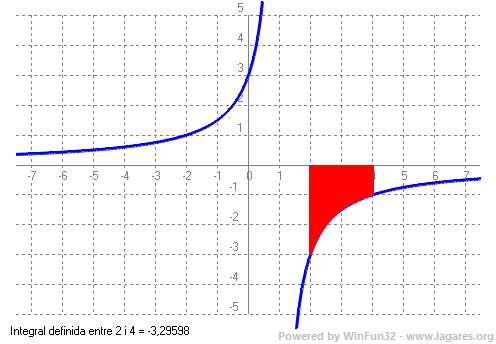


      Això no ho demana l'exercici.




      d) `\int (x dx)/(1+x^4)=\int dt/(2(1+t^2))=1/2\int dt/(1+t^2)=1/2 arctan(t)=1/2arctan(x^2)`

      `x^2=t => 2x=dt => x=dt/2`

      `\int_0 ^1 x/(1+x^4) dx=1/2[arctan(x^2)]0_^1=1/2[arctan(1^2)-arctan(0^2)]=`

      `1/2[arctan(1)-arctan(0)]=1/2(\pi/4-0)=\pi/8`


5- Calcula: `\int_-2 ^1 x^2e^xdx`. Per trobar una primitiva cal aplicar el mètode d'integració per parts dues vegades.


    SOLUCIÓ:
      `\int x^2e^xdx`

        `\int f'g = fg-\int fg'`

        `f'=e^x => f=e^x`

        `g=x^2 => g'=2x`


      `\int x^2e^xdx=x^2e^x -\int2xe^xdx =>x^2e^x -2\intxe^xdx`

        `\int xe^xdx`

          `\int f'g = fg-\int fg'`

          `f'=e^x => f=e^x`

          `g=x => g'=1`

        `\intxe^xdx=xe^x-\int e^xdx=xe^x- e^x`



      `\int x^2e^xdx=x^2e^x -\int2xe^xdx =>x^2e^x -2\intxe^xdx=x^2e^x -2(xe^x- e^x)=(x^2 -2x+2)e^x`

      `\int_-2^1 x^2e^xdx=[(x^2 -2x+2)e^x]_-2^1=(1^2 -2·1+2)e^1-((-2)^2 -2(-2)+2)e^(-2)=e-10/e^2`



6- Troba una primitiva de la funció `x^3/(x-2)` i calcula la integral d'aquesta funció en l'interval `[3,5]`.


    SOLUCIÓ

    `\int x^3/(x-2)dx`


      Dividim numerador per denominador, podem fer-ho per Ruffini:

           | 1 0 0 0
     | 
   2 |   2 4 8
-----+---------------
       1 2 4 8



    `x^3/(x-2)= x^2+2x+4 + 8/(x-2)`

    `\int x^3/(x-2)dx=\int (x^2+2x+4 + 8/(x-2))dx=x^3/3+x^2+4x-8ln|x-2|`


    `\int_3^5 x^3/(x-2)dx=[x^3/3+x^2+4x-8ln|x-2|]_3^5=`


    `(5^3/3+5^2+4·5-8ln|5-2|)-(3^3/3+3^2+4·3-8ln|3-2|)=`


    `(125/3+25+20-8ln(3))-(9+9+12-8ln(1))=`


    `(125/3+45-8ln|3|)-(30-8·0)=`


    `125/3+15-8ln(3)=170/3-8ln(3)`

7- Calcula `\int_0^2\sqrt{4-x^2}dx` utilitzant el canvi de variable: `x=2sin(t)`


    SOLUCIÓ:

      `\int\sqrt{4-x^2}dx`


      `x=2sin(t) => dx=2cos(t)dt`


      `\int \sqrt{4-x^2}dx=\int \sqrt{4-4sin^2(t)}·2cos(t)dt=2\int \sqrt{4(1-sin^2(t))}·cos(t)dt=`


      `4\int \sqrt{1-sin^2(t)}·cos(t)dt=4\int cos(t)·cos(t)dt=4\int cos^2(t)dt=`*


        Aquesta integral es pot calcular amb una de les fórmules de trigonometria de l'any passat,


        `cos^2(t) = (1+cos(2t))/2` o per parts. Aquí teniu la demostració. Que és:


        `\int cos^2tdt=1/2(sin(t)cos(t)+t)`



      *`=4\int cos^2(t)dt=4·1/2(sin(t)cos(t)+t)=2[sin(t)cos(t)+t]=`**


      `x=2sin(t) => sin(t)=x/2 => cos(t)=\sqrt{1-sin^2(t)}=\sqrt{1-x^2/4}` i `t=arcsin(x/2)`


      **`2[sin(t)cos(t)+t]=2[x/2·\sqrt{1-x^2/4}+arcsin(x/2)]=`


      `2[x/2·\sqrt{4/4-x^2/4}+arcsin(x)]=2[x/4·\sqrt{4-x^2}+arcsin(x/2)]`


      Finalment recordar que el que estem intentant calcular és:

      `\int_0^2\sqrt{4-x^2}dx=2[(x/4·\sqrt{4-x^2}+arcsin(x/2))]_0^2=`


      `2[(2/4·\sqrt{4-2^2}+arcsin(2/2))-(0/4·\sqrt{4-0^2}+arcsin(0/2))]=`


      `2[(0+arcsin(1))-(0+arcsin(0))]=2[\pi/2-0]=\pi`