Sigui la funció `f(x)=1/x`. a) Calculeu l’equació de la recta tangent a la gràfica de la funció `f` en el punt d’abscissa `x = 2`. [0,75 punts] Solució: Per calcular l'equació de la recta tangent en un punt cal un punt `(2,1/2)` i el pendent que el trobarem calculant la derivada en el punt `x=2`. `f'(x)=-1/x^2` que en el punt `f'(2)=-1/4` Per trobar l'equació de la recta tangent ho podem fer amb la punt pendent, `y-y_0=m(x-x_0)` `y-1/2=-1/4(x-2)` `y-1/2=-x/4+1/2` `y=-x/4+1/2+1/2` `y=-x/4+1` ANNEX: 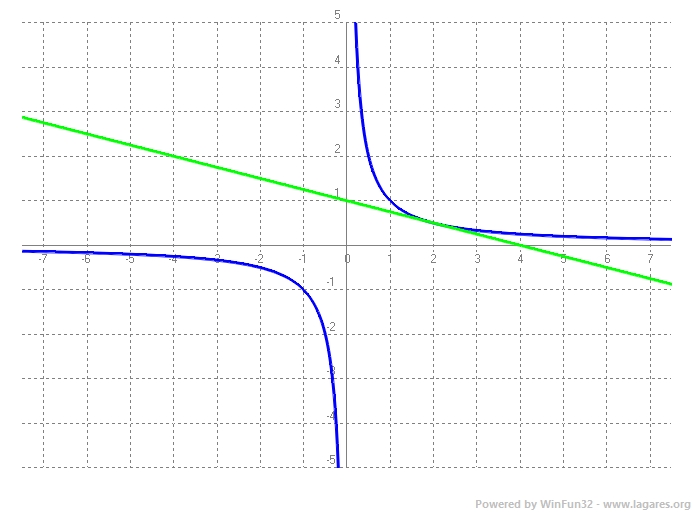Tot i no ser obligatori us mostrem la gràfica de la funció juntament amb la recta tangent demanada: b) Calculeu l’equació de la recta tangent a la gràfica de la funció `f` en el punt d’abscissa `x = k`, en què `k` és un nombre real positiu. [0,75 punts] Solució: Cal fer el mateix que hem fet abans, però en lloc de `x=2` posar `x=k`. El punt és `(k,1/k)` i `m=-1/k^2` L'equació punt pendent serà: `y-1/k=-1/k^2(x-k)` Si ho volem expressar amb l'equació explícita, com abans: `y-1/k=-x/k^2+1/k` `y=-x/k^2+1/k+1/k` `y=-x/k^2+2/k` c) Comproveu que, tal com es pot veure en la figura de sota, la recta de l’apartat `b` determina un triangle d’àrea constant amb els semieixos positius de coordenades. Calculeu aquesta àrea. [1 punt] 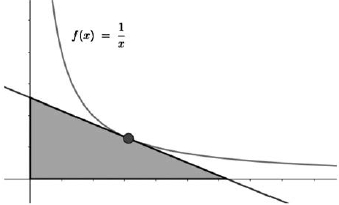Solució: 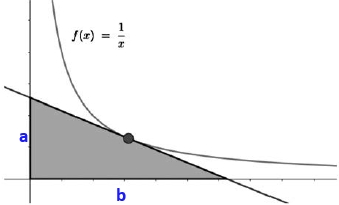Cal trobar la base, `b` i l'altura, `a`, per poder calcular l'àrea. Son els punts de tall amb els eixos Per trobar `a` cal trobar la imatge de `x=0 => a=-0/k^2+2/k=2/k` Per trobar, `b` cal trobar el punt de tall amb l'eix de les `x => y=0 =>` `0=-x/k^2+2/k` `x/k^2=2/k` `x=2k^2/k` `x=2k => b=2k` Finalment per trobar l'àrea del triangle només cal multiplicar la base · l'altura i dividir-ho per `2`. Àrea `= (2k·2/k)/2 = 2` unitats quadrades I comprovem que no depèn del punt `k` triat.