Matemàtiques - 4t ESO - Funcions 10 b. Funcions polinòmiques i racionals 1- Dibuixa amb els programa funcions o el Geogebra les funcions de 2n grau següents: `f(x) = (x-1)^2 - 2` `g(x) = (x+2)^2 + 1` `h(x) = (x+3)^2 - 3` `k(x) = 2(x-1)^2 - 2` Explica com és la gràfica de les funcions de segon grau en funció dels tres coeficients que hem escrit. Suggeriments, pots experimentar dibuixant, amb un dels dos programes funcions de segon grau similars. SOLUCIÓ: `f(x) = (x - 1)^2 - 2`. Blava. És com `x^2`, però desplaçada `1` unitat a la dreta i `2` avall. El vèrtex es troba en el punt `(1, -2)`. `g(x) = (x + 2)^2 + 1`. Verda. És com `x^2`, però desplaçada `2` unitats a l'esquerra i `1` amunt. El vèrtex es troba en el punt `(-2, 1)`. `h(x) = (x + 3)^2 - 3`. Fucsia. És com `x^2`, però desplaçada `3` unitats a l'esquerra i 3 avall. El vèrtex es troba en el punt `(-3, -3)`. `k(x) = 2(x - 1)^2 - 2`. Blau cel. És com `2x^2`, però desplaçada `1` unitat a la dreta i `2` avall. El vèrtex es troba en el punt `(1, -2)`. 2- Dibuixa en dos finestres del programa funcions o Geogebra les funcions de 2n grau següents: (a l'enunciat hi havia un error, hi poso l'original perquè si no, no es veu el que es volia que veiéssiu) `f(x) = (x-2)^2 - 1` `g(x) = x^2 - 4x + 3` Explica perquè passa el que veus. 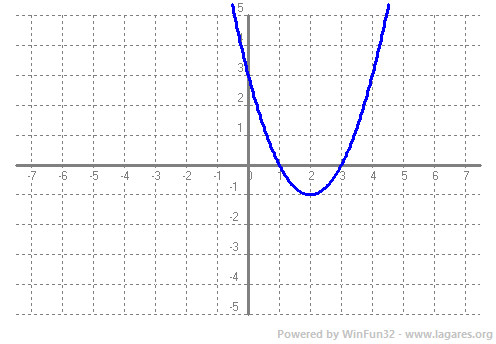SOLUCIÓ: `f(x) = (x-2)^2 - 1` `g(x) = x^2 - 4x + 3` Són la mateixa funció ja que, `(x-2)^2 - 1 =` `x^2-4x+4-1 =` `x^2-4x+3` 3- Si una persona triga en pintar un mur 100 dies. Digues: a- Quant trigarien 2 persones? 4 persones? 5 persones? 10 persones? SOLUCIÓ: Hem de suposar que `2` persones trigaran la meitat. Ho sigui: 2 50 4 25 5 20 10 10 b- Dibuixa una gràfica que relacioni el que es triga a pintar el mur en funció del número de persones que hi treballen. SOLUCIÓ: c- Sabries escriure la fórmula de la funció que descriu aquestes dades que han sortit? SOLUCIÓ: `y=100/x` d- Amb un dels dos programes que coneixes, dibuixa la gràfica a partir de la fórmula que has trobat. Segurament hauràs de canviar l’escala, com a mínim la de l’eix `y`. SOLUCIÓ: e- Hi ha un tros de la gràfica que surt representada que no ens és útil. Quin és? SOLUCIÓ: La negativa, ja que no té cap sentit un nombre negatiu de treballadors. f- Podrien tenir sentit els valor de la gràfica amb x més petits que 1? SOLUCIÓ: Tampoc no té gaire sentit, ja que no és pot tenir menys d'un treballador (amb permís de que un treballador treballi menys que un dia sencer ;-). 4- Dibuixa amb un dels dos programes la funció: `f(x)=1/x` Quan val la imatge de `0`? Quin és el seu domini? I el seu recorregut? SOLUCIÓ: `f(0)=1/0` no existeix, ja que no es pot dividir per `0`. Tant el domini com el recorregut són, `R-{0}` 5- Dibuixa la funció: `f(x)=(-1)/x` SOLUCIÓ: És la mateixa que l'anterior, però simètrica respecte qualsevol dels dos eixos de coordenades. 6- Ara dibuixa les funcions: `i(x)=(0'5)/x`, `f(x)=1/x`, `g(x)=2/x`, `h(x)=5/x` Què hi observes? SOLUCIÓ: Estan dibuixades amb el mateix ordre que estan escrites a dalt. S'observa que tenen la mateixa forma, però quan més gran és el nombre del numerador, més separada està dels eixos. 7- Dibuixa les funcions: `f(x)=1/x+2`, `g(x)=1/x-1`, `h(x)=-1/x+3` Què hi observes? Calcula el domini i el recorregut de cadascuna. SOLUCIÓ: `f(x)=1/x+2` Igual que la `1/x`, però pujada `2` unitats. Domini, `R-{0}`; Recorregut, `R-{2}`. `g(x)=1/x-1` Igual que la `1/x`, però baixada `1` unitat. Domini, `R-{0}`; Recorregut, `R-{1}`. `h(x)=-1/x+3` Igual que la `(-1)/x`, però pujada `3` unitats. Domini, `R-{0}`; Recorregut, `R-{3}`. 8- Dibuixa les funcions: `f(x)=1/(x-1)`, `g(x)=1/(x+2)`, `h(x)=1/(x-3)` Què hi observes? Calcula el domini i el recorregut de cadascuna. SOLUCIÓ: `f(x)=1/(x-1)` Igual que la `1/x`, però moguda a la dreta `1` unitat. Domini, `R-{1}`; Recorregut, `R-{0}`. `g(x)=1/(x+2)` Igual que la `1/x`, però moguda a l'esquerra `2` unitats. Domini, `R-{-2}`; Recorregut, `R-{0}`. `h(x)=1/(x-3)` Igual que la `(-1)/x`, moguda a la dreta `3` unitats. Domini, `R-{3}`; Recorregut, `R-{0}`. 9- Dibuixa: `f(x)=1/(x-1)+2`, `g(x)=1/(x+2)-1`, `h(x)=1/(x-3)+0'5` Què hi observes? Calcula el domini i el recorregut de cadascuna. SOLUCIÓ: `f(x)=1/(x-1)+2` Igual que la `1/x`, però moguda a la dreta `1` i `2` amunt. Domini, `R-{1}`; Recorregut, `R-{2}`. `g(x)=1/(x+2)-1` Igual que la `1/x`, però moguda a l'esquerra `2` i `1` avall. Domini, `R-{-2}`; Recorregut, `R-{-1}`. `h(x)=1/(x-3)+0'5` Igual que la `(-1)/x`, moguda a la dreta `3` unitats i `0'5` amunt. Domini, `R-{3}`; Recorregut, `R-{0'5}`.