|
- Si un animal unicel·lular es reprodueix per bipartició cada hora, quants animals d'aquesta espècie tindrem al cap d'1, 2, 3, 4, 5, 6 hores? Dibuixa'n la gràfica. Escriu la fórmula de la funció que relaciona el nombre d'animals unicel·lulars amb el temps. Amb el programa funcions dibuixa la gràfica de la funció que acabes de trobar i compara-la amb la que havies construït a mà. SOLUCIÓ:  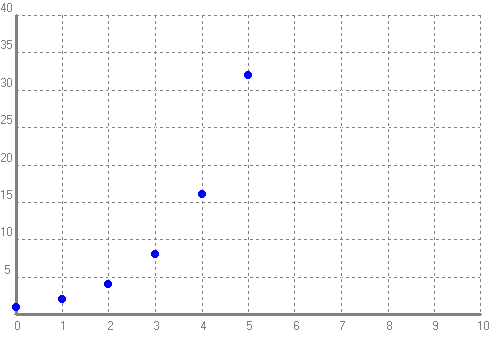 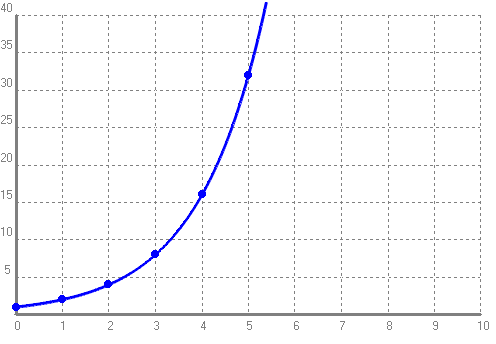 - Suposa que una persona té 1600€ i cada dia es gasta la meitat del que té. Calcula quants diners tindrà al cap de 6 dies. Quin dia tindrà menys de 150€? Escriu la fórmula de la funció que diu els diners que li resten en funció dels dies que van passant. SOLUCIÓ: 
- Si tenim 100€ i els posem en un banc al 7% d'interés anual. Podries dir quants diners tindrem al cap d'un any?, al cap de 2?, de 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40 (escriu una taula amb els resultats)? Dibuixa'n la gràfica. Sabries escriure la fórmula de la funció que relaciona els diners que tinc en el banc en funció del nombre d'anys transcorreguts? Amb el programa funcions dibuixa la gràfica de la funció que acabes de trobar i compara-la amb la que havies construït a mà. Si en el tema 1 no havies vist, The Most IMPORTANT Video You'll Ever See, ara és un molt bon altre moment per fer-ho. Cal recordar lo explicat en el primer tema sobre l'interès compost. `C_f=C_i(1+i)^t`. SOLUCIÓ:
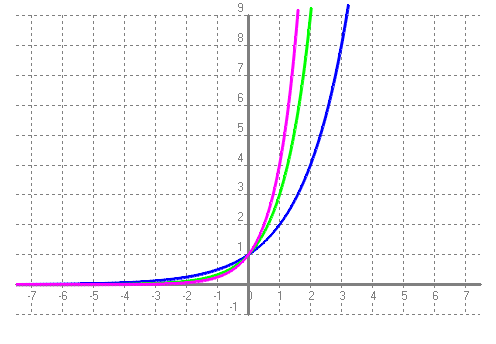
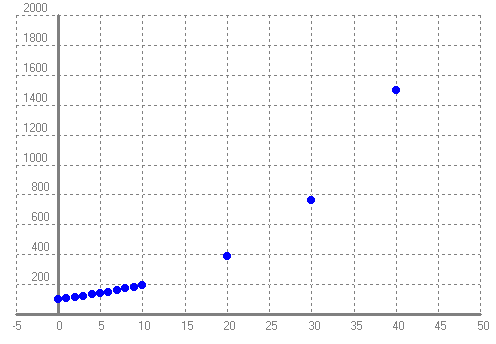 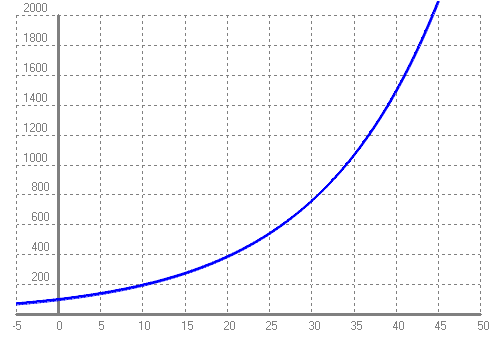 - Si tenim un cotxe que val 10000 i se sap que cada any perd el 10% del seu valor, pots respondre a les mateixes preguntes que se't fan en el problema anterior? Què hi ha de semblant? Què hi ha de diferent? SOLUCIÓ: Cal recordar que si una cosa perd el `10%` de valor és com si tingués un descompte del `10%`. Aplicar un descompte del `10%` es calcula multiplicant per `1-10/100=0'9`. O sigui la fórmula de la funció preu és, `P(x)=10000·0'9^t`. I la taula serà: 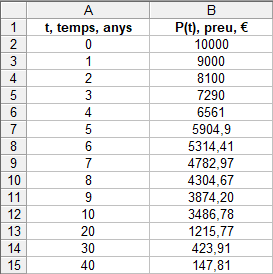 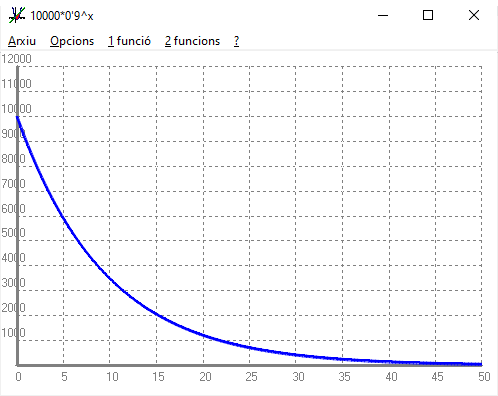 - Amb l'ajuda del programa funcions: a) Dibuixa en una gràfica les funcions `f(x) = 2^x`, `g(x) = 3^x` i `h(x) = 4^x`. SOLUCIÓ:
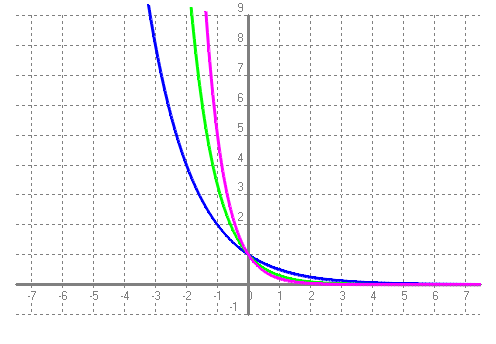
 b) Dibuixa en una gràfica les funcions `f(x) = 0'5^x`, `g(x) = 0'3^x` i `h(x) = 0'2^x`. SOLUCIÓ:
 c) Dibuixa en una gràfica la funció `f(x) = 1^x`. Què hi observes? SOLUCIÓ: 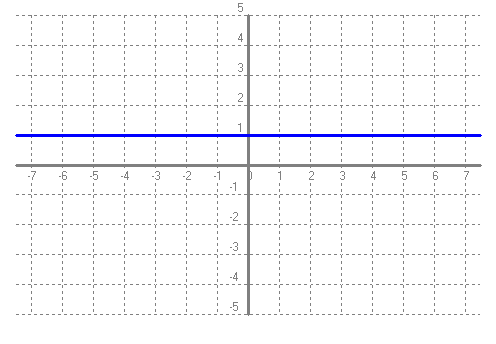
d) Què creus que què passa amb la funció `f(x) = (-2)^x` o amb la funció `g(x) = (-0'25)^x`. SOLUCIÓ:
Per la qual cosa la funció exponencial, `f(x)=b^x`, només la estudiarem per bases, `b`, positives. e) Les funcions que acabes d'estudiar, de la forma `y = b^x`, se'n diuen funcions exponencials. Què ha de complir la base, `b`, i quina forma té la gràfica segons sigui el seu valor? SOLUCIÓ:
I pels apartats, a i b, hem descobert que si la base és més gran que `1` les funcions són creixents i si la base és més petita que `1` les funcions són decreixents. - Si el creixement de la població humana fos del 8% anual, podries explicar què passarà d'aquí 9 anys? SOLUCIÓ:
- Si cada any gastem el 5% del petroli que queda, pots calcular quant de petroli quedarà d'aquí 13 anys? SOLUCIÓ:
Per la qual cosa per saber el petroli que queda al cap d'`1` any cal multiplicar el que hi ha aquest any per, `0'95`. Si passen 13 anys, cal multiplicar per `0'95^13 \approx 0'51`. O sigui en quedarà la meitat del que teníem al principi. - Si, per exemple, una cosa augmenta el 10% anual, pots explicar una forma de saber quan el seu valor s'ha duplicat? i quan s'haurà triplicat? SOLUCIÓ:
Si volem saber quants anys han de passar perquè una cosa es dupliqui, hem de veure quin valor de `t` ha de tenir la següent expressió, `1'1^t=2`. Això és una equació en que l'incògnita està a l'exponent. De moment no sabem resoldre-la, per fer-ho cal conèixer els logaritmes i les seves propietats. Però això no ho aprendrem fins més endavant. Com ho podem resoldre-ho ara? De moment de dues maneres: 1-Fent una taula i mirant quina `x` correspon a la `y=2` i quina `x` correspon a la `y=3`. 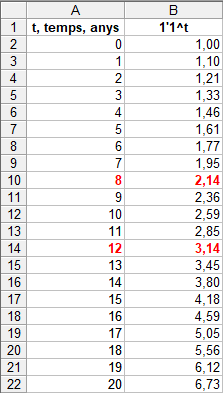 I mirant a la taula observem que si una cosa creix al `10%` es duplicarà entre el 7è i el 8è any. 2-Buscant l'antiimatge del `2` i del `3` en el programa Funcions per a Windows, (WinFun32). 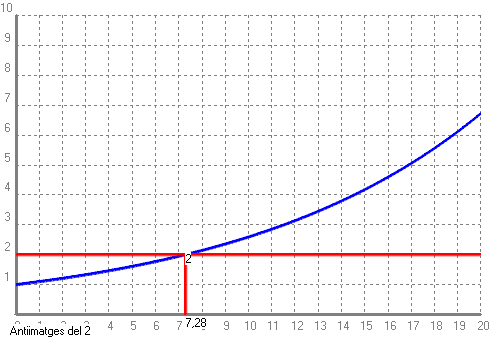 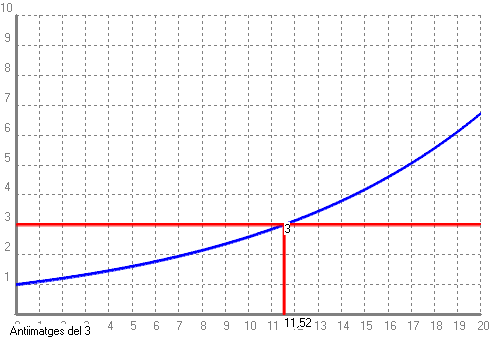 - Poso 1000€ al 10% anual en un compte d'un banc quan el seu valor es duplicarà? i quan es triplicarà? Pots dibuixar la gràfica amb el programa funcions i fer servir l'opció antiimatge. SOLUCIÓ:
I `1000€` al `10%` d'interès anual és convertiran en `3000€` al cap de `11'52` anys. Els dibuixos no caldria posar-los, però si ho voléssim fer, ho podem fer amb la funció `f(x)=1000·1'1^x`, tot i que el raonament del problema anterior és perfectament vàlid. En aquest cas caldrà canviar els valors de l'eix `y`. 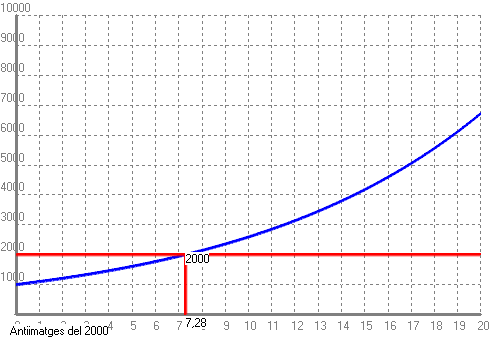 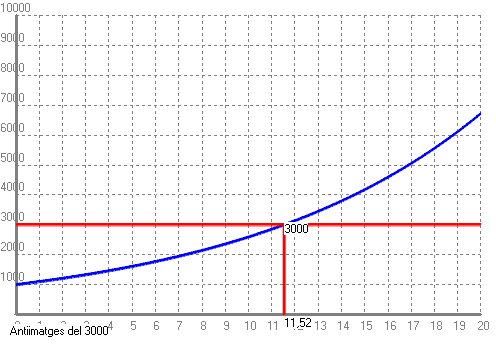 - Per resoldre els dos problemes anteriors ho hem hagut de fer d'una forma molt feixuga. Seria més interessant poder resoldre directament l'equació 1'10x = 2 sabent aïllar directament la x que està en l'exponent. Per això necessitem una nova eina matemàtica anomenada logaritme. a) Sabries dir quina és l'exponent que he d'elevar 2 perquè doni 8, i 16, i 64, i 2, i 1, i 0'5, i 0'25, i 40 (sabries donar-ne una aproximació). SOLUCIÓ: 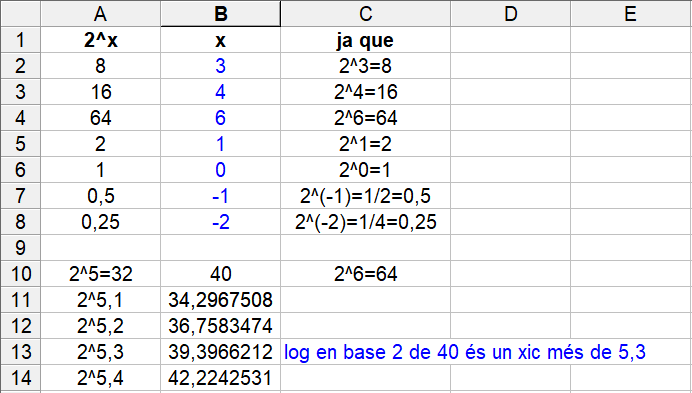 b) Sabries dir quina és l'exponent que he d'elevar 3 perquè doni 9, i 27, i 81, i 243, i 3, i 1, i 30 (sabries donar-ne una aproximació). SOLUCIÓ: 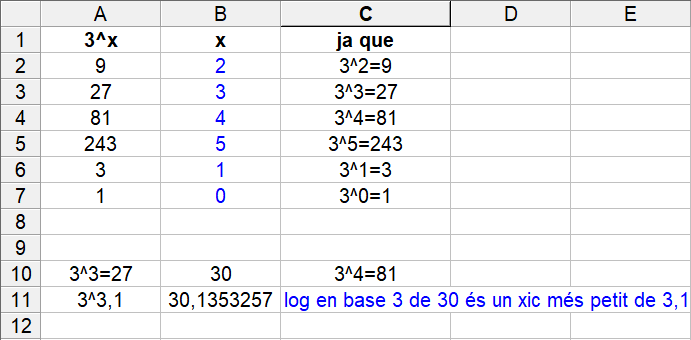 c) Sabries dir quina és l'exponent que he d'elevar 10 perquè doni 100, 1000, 1000000, 10, 1, 0'1, 0'001, 0'000001, i 20 (sabries donar-ne una aproximació). SOLUCIÓ: 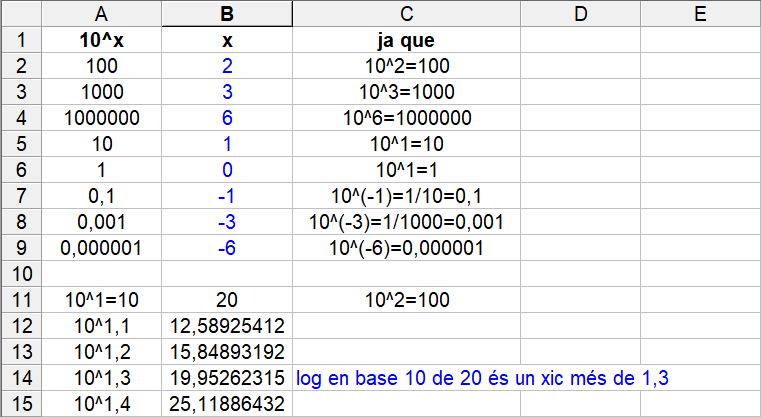 - Calcula: a) Logaritme en base 2 de 8, 16, 64, 2, 1, 0'5, 0'25, 40 (sabries donar-ne una aproximació). SOLUCIÓ: Com que el logaritme en una certa base, és l'exponent al que hem d'elevar la base, les respostes a aquestes preguntes són le mateixes que a l'exercici anterior. 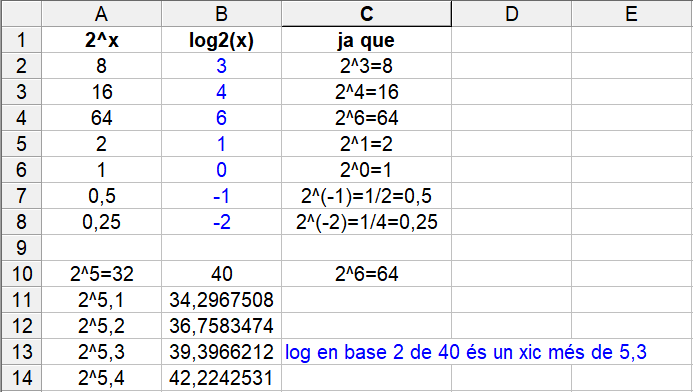 b) Logaritme en base 3 de 9, 27, 81, 243, 3, 1, 30 (sabries donar-ne una aproximació). SOLUCIÓ: 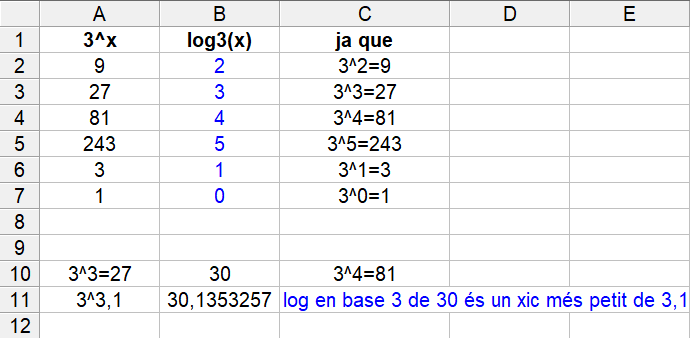 c) Logaritme en base 10 de 100, 1000, 1000000, 10, 1, 0'1, 0'001, 0'000001, 20 (sabries donar-ne una aproximació). SOLUCIÓ: 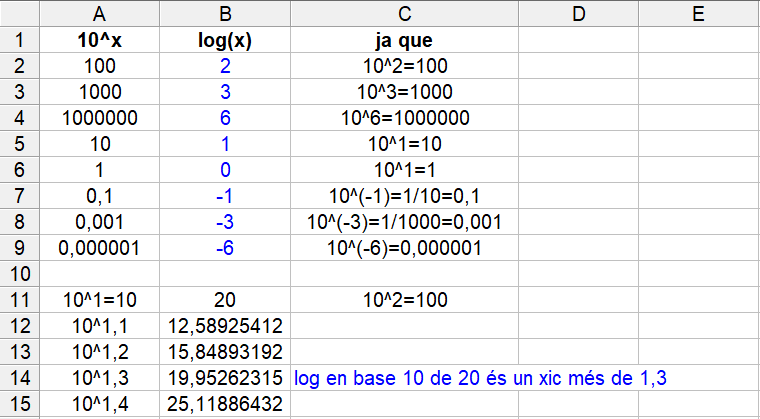 - Fent servir la calculadora calcula els logaritmes en base 10 (decimals) de 100, 1000, 1000000, 10, 1, 0'1, 0'001, 0'000001, 20, 2014, -10, -100. SOLUCIÓ: 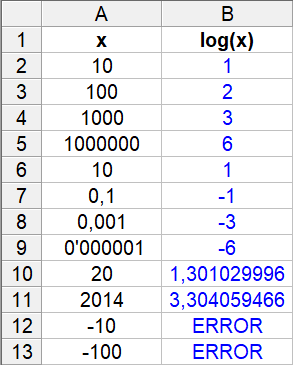 - Calcula el següent: a) log(100), log(1000) i log(100000). Et faig notar que 100 · 1000 = 100000. SOLUCIÓ: Aquest exercici pot semblar una mica estrany, però bàsicament tracta de descobrir una interessant propietat que tenen els logaritmes de convertir, en certa manera, un producte en una suma. En realitat pot convertir el logaritme d'un producte en suma de logaritmes `log(100)=2` `log(1000)=3` `log(100000)=5` Comprovem-ho: `log(100 · 1000)=log(100000)=5=2+3=log(100)+log(1000)` b) log2(8), log2(16) i log2(128). Recorda que 8 · 16 = 128. SOLUCIÓ: `\log_2 8=3` `\log_2 16=4` `\log_2 128=7` Veiem que també es compleix: `\log_2 (8·16)=\log_2 128=7=3+4=\log_2 8 + \log_2 16` c) log2(2), log2(128) i log2(256). Recorda que 2 · 128 = 256. SOLUCIÓ: `\log_2 2=1` `\log_2 128=7` `\log_2 256=8` Veiem que també es compleix: `\log_2 (2·128)=\log_2 256=8=1+7=\log_2 2 + \log_2 128` d) log3(27), log3(9) i log3(243). Recorda que 27 · 9 = 243. SOLUCIÓ: `\log_3 27=3` `\log_3 9=2` `\log_3 243=5` Veiem que també es compleix: `\log_3 (27·9)=\log_2 243=5=3+2=\log_3 27 + \log_3 9` e) log(10), log(100) i log(1000). SOLUCIÓ: `log(10)=1` `log(100)=2` `log(1000)=3` Veiem que també es compleix: `log(10·100)=log(1000)=3=1+2=log(10)+log(100)` f) log5(25), log5(25) i log5(625). SOLUCIÓ: `\log_5 25=2` `\log_5 25=2` `\log_5 625=4` Veiem que també es compleix: `\log_5 (25·25)=\log_5 625=4=2+2=\log_5 25 + \log_5 25` g) log(1000), log(0'1) i log(100). SOLUCIÓ: `log(1000)=3` `log(0'1)=-1` `log(100)=2` Veiem que també es compleix: `log(1000·0'1)=log(100)=2=3+(-1)=log(1000)+log(0'1)` h) log(10000), log(0'001) i log(10). SOLUCIÓ: `log(10000)=4` `log(0'001)=-3` `log(10)=1` Veiem que també es compleix: `log(10000·0'001)=log(10)=1=4-3=log(10000)+log(0'001)` i) log2(64), log2(0'5) i log2(32). SOLUCIÓ: `\log_2 64=6` `\log_2 0'5=\log_2 (1/2)=-1` `\log_2 32=5` Veiem que també es compleix: `\log_2 (64·0'5)=\log_2 32=5=6+(-1)=\log_2 64 + \log_2 0'5` j) Dels càlculs que acabes de fer, en saps trobar una propietat en el càlcul del logaritme del producte? SOLUCIÓ: - Calcula el següent: a) log(1000), log(100) i log(10). Et faig notar que 1000 / 100 = 10. SOLUCIÓ: Aquest exercici pot semblar una mica estrany, però havent fet l'anterior, ja no ho és tant. Bàsicament es tracta de descobrir una altra interessant propietat que tenen els logaritmes de convertir, en certa manera, un quocient en una diferència. En realitat pot convertir el logaritme d'un quocient en resta de logaritmes `log(1000)=3` `log(100)=2` `log(10)=1` Comprovem-ho: `log(1000/100)=log(10)=1=3-2=log(1000)-log(100)` b) log2(64), log2(2) i log2(32). Recorda que 64 / 2 = 32. SOLUCIÓ: `\log_2 64=6` `\log_2 2=1` `\log_2 32=5` Veiem que també es compleix: `\log_2 (64/2)=\log_2 32=5=6-1=\log_2 64 - \log_2 2` c) log2(256), log2(8) i log2(32). SOLUCIÓ: `\log_2 256=8` `\log_2 8=3` `\log_2 32=5` Veiem que també es compleix: `\log_2 (256/8)=\log_2 32=5=8-3=\log_2 256 - \log_2 8` d) log3(81), log3(9) i log3(9). SOLUCIÓ: `\log_3 81=4` `\log_3 9=2` `\log_3 9=2` Veiem que també es compleix: `\log_3 (81/9)=\log_3 9=2=4-2=\log_2 81 - \log_2 9` e) log(100), log(100) i log(1). SOLUCIÓ: `log(100)=2` `log(10)=1` Comprovem-ho: `log(100/100)=log(1)=0=2-2=log(100)-log(100)` f) log5(625), log5(5) i log5(125). SOLUCIÓ: `\log_5 625=4` `\log_5 5=1` `\log_5 125=3` Veiem que també es compleix: `\log_3 (625/5)=\log_5 125=3=4-1=\log_5 625 - \log_5 5` g) log(100), log(100000) i log(0'001). SOLUCIÓ: `log(100)=2` `log(100000)=5` `log(0'001)=-3` Comprovem-ho: `log(100/100000)=log(0'001)=-3=2-5=log(100)-log(100000)` h) log(0'1), log(10) i log(0'01). SOLUCIÓ: `log(0'1)=-1` `log(10)=1` `log(0'01)=-2` Comprovem-ho: `log((0'1)/10)=log(0'01)=-2=-1-1=log(0'1)-log(10)` i) log2(8), log2(0'5) i log2(16). SOLUCIÓ: `\log_2 8=3` `\log_2 0'5=-1` `\log_2 16=4` Veiem que també es compleix: `\log_2 (8/(0'5))=\log_2 16=4=3-(-1)=\log_2 8 - \log_2 0'5` j) Dels càlculs que acabes de fer, en saps trobar una propietat en el càlcul del logaritme d'una divisió? SOLUCIÓ: - Calcula el següent: a) log(10), log(103). SOLUCIÓ: Aquí de forma semblant que en els exercicis anteriors descobrirem una nova propietat dels logaritmes quan es tracti de calcular el logaritme d'una potència. `log(10)=1` `log(10^3)=3` Comprovem-ho: `log(10^3)=3=3.1=3·log(10)` b) log2(2), log2(25). SOLUCIÓ: `\log_2 2=1` `\log_2 2^5=5` `\log_2 2^5=5·1=5·\log_2 2` c) log2(4), log2(64). Recorda que 43 = 64 SOLUCIÓ: `\log_2 4=2` `\log_2 64=6=\log_2 4^3` `\log_2 4^3=6=3·2=3·\log_2 4` d) log3(9), log3(81). Recorda que 92 = 81. SOLUCIÓ: `\log_3 9=2` `\log_3 81=4=\log_3 9^2` `\log_3 9^2=4=2·2=2·\log_3 9` e) log(100), log(1004). SOLUCIÓ: `log(100)=2` `log(100^4)=log(10^8)=8` `log(100^4)=8=4·2=4·log(100)` f) log3(27), log3(272). SOLUCIÓ: `\log_3 27=3` `\log_3 27^2=\log_3 3^6=6` `\log_3 27^2=6=2·3=2·\log_3 27` g) log(10), log(0'01). Recorda que 10-2 = 0'01. SOLUCIÓ: `log(10)=1` `log(0'01)=log(10^(-2))=-2` `log(10^(-2))=-2=-2·1=-2·log(10)` h) log(5), log(54). Aquets càlculs pots fer-los amb la calculadora. SOLUCIÓ: `log 5=0'69897` `log 5^4=2'79588` `log 5^4=4·log 5=4.0'69897=2'79588` i) log(4), log(1/16). SOLUCIÓ: `log(4)=0'60206` `log(1/16)=-1'20412` `log(1/16)=log(4^(-2))=-2·log(4)=-2·0'60206=-1'20412` j) Dels càlculs que acabes de fer, en saps trobar una propietat en el càlcul del logaritme d'una potència? SOLUCIÓ: - Escriu les fórmules les propietats (totes) que acabes de trobar. També escriu la fórmula del canvi de base. SOLUCIÓ:
Propietats:
2-`\log_b (a/c)=\log_b (a)-\log_b (c)` 3-`\log_b (a^x)=x·\log_b (a)` 4-`\log_b root(n){a}=\log_b a^(1/n)=1/n·\log_b a` (logaritme d'una arrel és conseqüència de l'anterior. 5-`\log_b a=\log_c a/\log_c b` (Fórmula del canvi de base. Sense demostració. No surt de las propietats anteriors, calia trobar-ho al llibre). - En un exercici anterior dèiem: Si una cosa augmenta el 10% anual, quant de temps trigarà a duplicar-se.
SOLUCIÓ: Pel que acabem de dir a dalt: `t = log(2)/log(1'1)=7,27` anys. b) Si una cosa augmenta el 10% anual, quant de temps trigarà a triplicar-se?. SOLUCIÓ: Pel que acabem de dir a dalt: `t = log(3)/log(1'1)=11,53` anys. c) Poso 1000€ al 10% anual en un compte d'un banc quan el seu valor es duplicarà? SOLUCIÓ: Pel que acabem de dir a l'apartat a: `7,27` anys. d) Poso 1000€ al 5% anual en un compte d'un banc quant de temps trigarà en convertir-se en 1500€? SOLUCIÓ: `C_f=C_i·(1+i)^t` `1000·1'05^t=1500` `1'05^t=1500/1000` `1'05^t=1'5` `log(1'05^t)=log(1'5)` `t·log(1'05)=log(1'5)` per la propietat `4` dels logaritmes. `t=log(1'5)/log(1'05)=8'31` anys e) La població mundial, del dia 8 de setembre de 2014 a 2/4 de 6 de la tarda, era de 7.190.760.386 habitants. Si l'increment anual fos del 1'7%, quant trigarà el món a tenir 10.000.000.000 de persones? SOLUCIÓ: `P_f=P_i·(1+i)^t` `7190760386·1'017^t=10000000000` `1'017^t=10000000000/7190760386` `1'017^t=1,390673` `log(1'017^t)=log(1,390673)` `t·log(1'017)=log(1,390673)` `t=log(1,390673)/log(1'017)=19'57` anys f) Mira aquí la població d'avui. Calcula quin % ha crescut fins ara la població respecte el 8 de setembre de 2014 a 2/4 de 6 de la tarda. SOLUCIÓ: 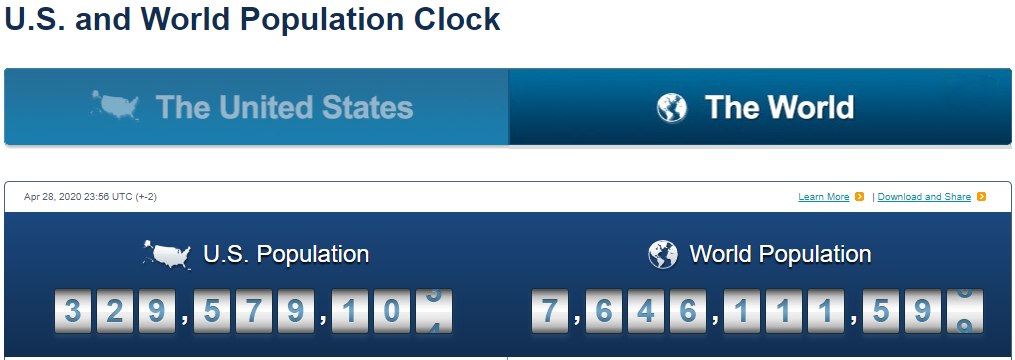 Calculadora de tiempo entre dos fechas: 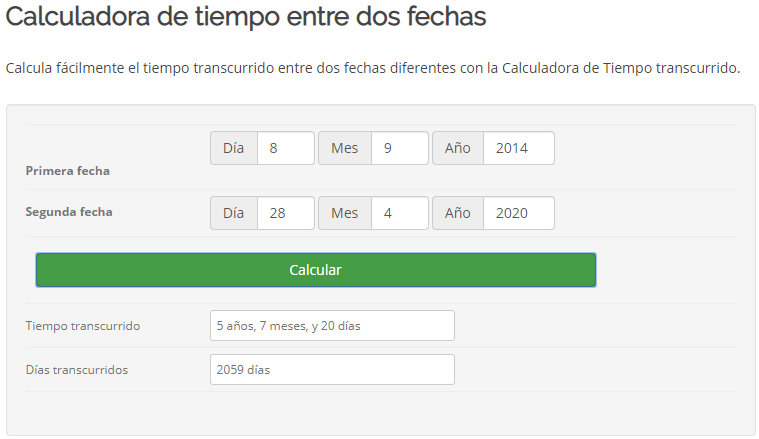 Calculem quants any són 2059 dies,`2059/365=5'64` anys. La població ha augmentat en `7.190.760.386` a `7.646.111.599` = `455.351.213` d'habitants. En mitjana el `%` que ha augmentat és de, `455351213/7646111599=0,059553`. O dividim pel nombre d'anys transcorreguts, `(0'059553)/(5'64) = 0'010559 = 1'0559%` de creixement anual mitjà. (Aquesta forma de calcular el % mitjà de creixement anual no és estrictament correcta, però per no complicar el raonament ho deixem així). g) Calcula de nou l'apartat e fent servir el resultat de l'apartat f. SOLUCIÓ: `P_f=P_i·(1+i)^t` `7646111599·1'0106^t=10000000000` `1'0106^t=10000000000/7646111599` `1'0106^t=1,307854` `log(1'0106^t)=log(1,307854)` `t·log(1'0106)=log(1,307854)` `t=log(1,307854)/log(1'0106)=25'45` anys - Una moto nova val 4500 €, si la seva desvalorització és del 25% anual. Quant de temps trigarà a valer 1000€? i 500€?. SOLUCIÓ: `P_f=P_i·(1+i)^t` a) `4500·(1-0'25)^t=1000` `4500·(0'75)^t=1000` `0'75^t=1000/4500` `log(0'75^t)=log(1000/4500)` `t=log(1000/4500)/log(0'75)=5'23` b) Podem aprofitar el desenvolupament de l'apartat, `a`, canviant el 1000 per 500. `t=log(500/4500)/log(0'75)=7'64` anys - A mà, dibuixa la gràfica de la funció logaritme en base 2, f(x) = log 2(x). Podries dir quin és el seu domini, el seu recorregut, els punts de tall i explica el seu comportament. SOLUCIÓ: 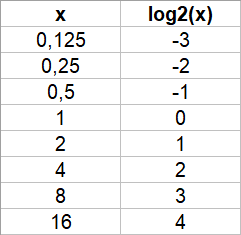 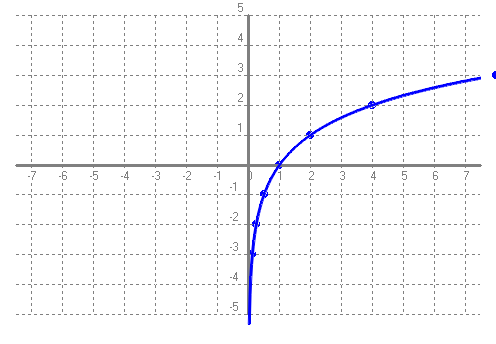 Domini: `(0,+\infty)`. Recorregut: `(-\infty,+\infty)` o sigui tots els `R`. Tall amb l'eix de les `x`, `(1,0)`. Tall mb l'esi `y`, no en té. És una funció que sempre és creixent. - A mà, dibuixa la gràfica de la funció logaritme en base (1/2), f(x) = log (1/2)(x). Podries dir quin és el seu domini, el seu recorregut, els punts de tall i explica el seu comportament. SOLUCIÓ: 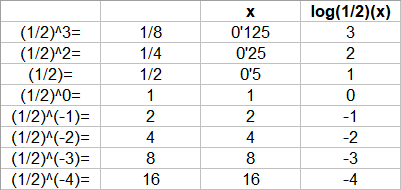 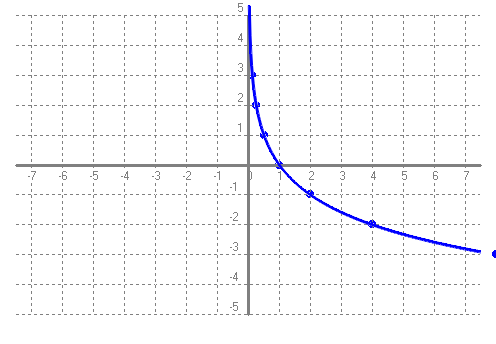 Domini: `(0,+\infty)`. Recorregut: `(-\infty,+\infty)` o sigui tots els `R`. Tall amb l'eix de les `x`, `(1,0)`. Tall mb l'esi `y`, no en té. És una funció que sempre és decreixent. Totes les gràfiques que venen a continuació acaben en una asímptota vertical encara que en els dibuixos no s'acabi d'apreciar. Quan no es veu l'asímptota vertical és l'eix de les `y`. L'eix vertical. - Amb el programa funcions dibuixa les gràfiques de les funcions: a) f(x) = log3(x) 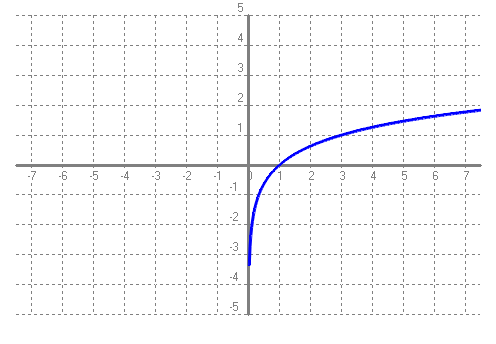 b) g(x) = log0'3(x) 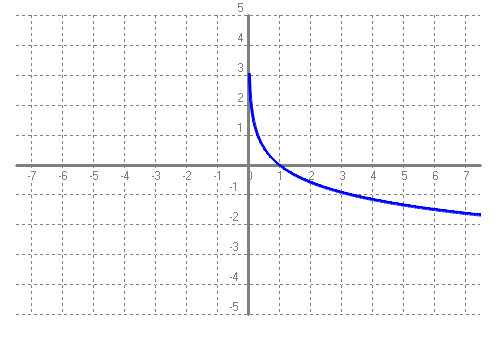 c) h(x) = log(x) 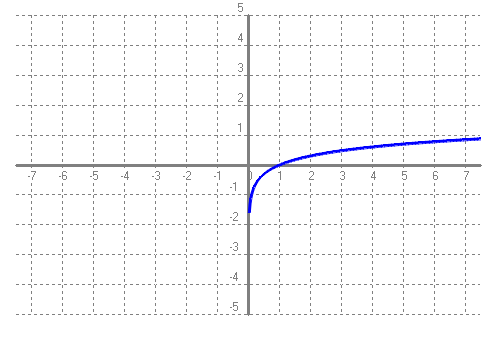 d) i(x) = ln(x) 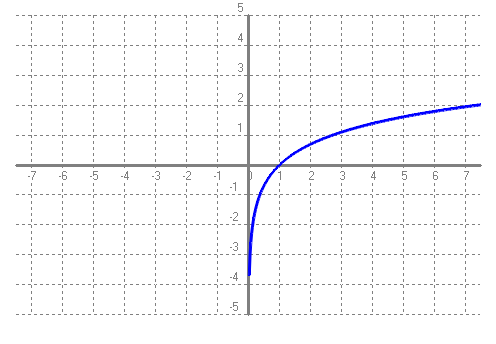 e) f(x) = log0'1(x). Per dibuixar una funció logarítmica en una altra base podem fer servir la fórmula del canvi de base logb(x) = log(x) / log(b). 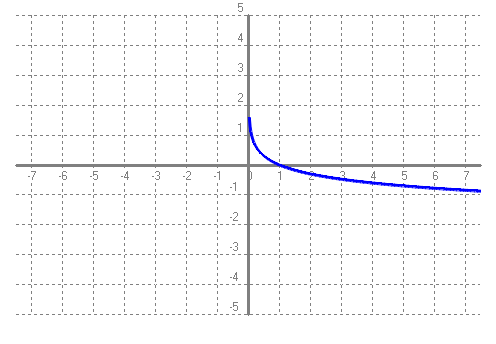 f) Podries explicar la diferència de comportament de les gràfiques segons el valor de la base? SOLUCIÓ:
Si la base és `<1` les funcions són decreixents. g) Per què no demanem la funció logarítmica en base un nombre negatiu? o 0? o 1? SOLUCIÓ:
Base negativa, preguntar-nos per a quin nombre hem d'elevar `-2` perquè doni 2 veiem que no pot ser. Al haver-hi molts de números que no es pot calcular el seu logaritme en una base negativa, no els considerem. - Amb el programa funcions dibuixa les gràfiques de les funcions: a) f(x) = log(x - 1) 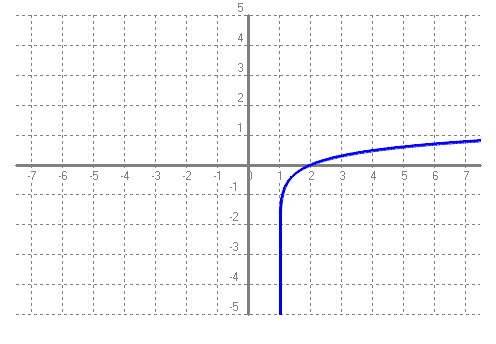 b) g(x) = log(x + 2) 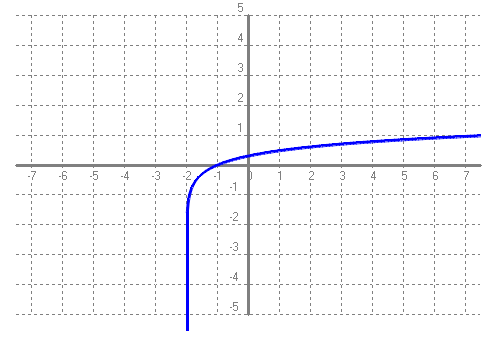 c) h(x) = log(x) - 3  d) i(x) = ln(x) + 1 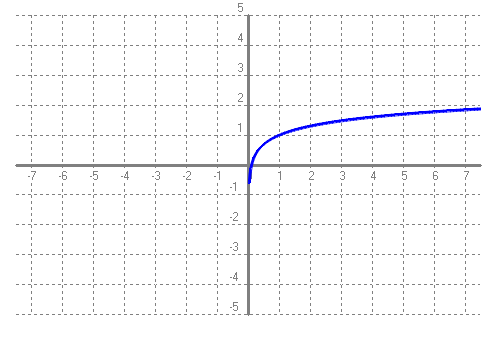 e) f(x) = log2(x) - 3 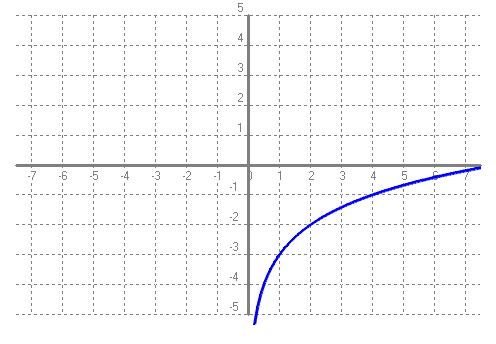 f) Aquest comportament, al fer els canvis que acabem de fer, ja l'havíem vist en altres ocasions, que el pots explicar? SOLUCIÓ: Si tenim una funció i canviem `x` per `(x-a)` això li provoca un desplaçament cap a la dreta si `a>0` i cap a l'esquerra si `a<0` Si a canviem `f(x) -> f(x)+a` el que provoca és un desplaçament vertical cap a dalt si `a>0` i cap a baix si `a<0`. - Tornem a la funció exponencial. Pots explicar que tenen a veure les freqüències de les notes musicals amb la funció exponencial? SOLUCIÓ: 1-  Les notes que sonen quan toquem aquestes tecles, totes, es diuen, La. I si mirem la forma de l'ona per cada un dels sons observarem el següent: 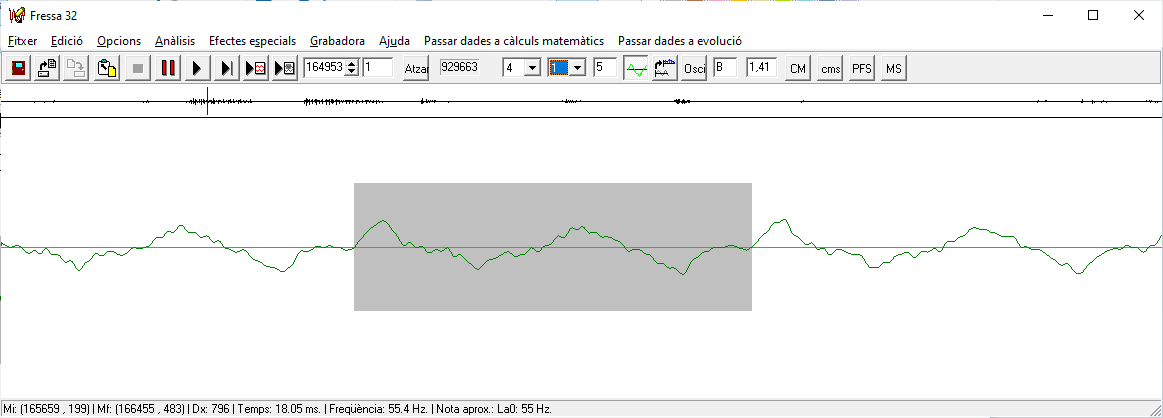 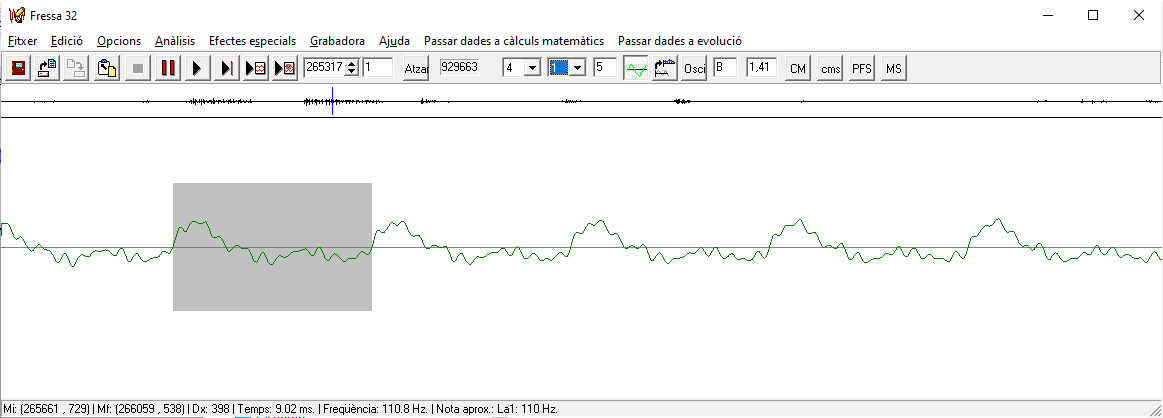 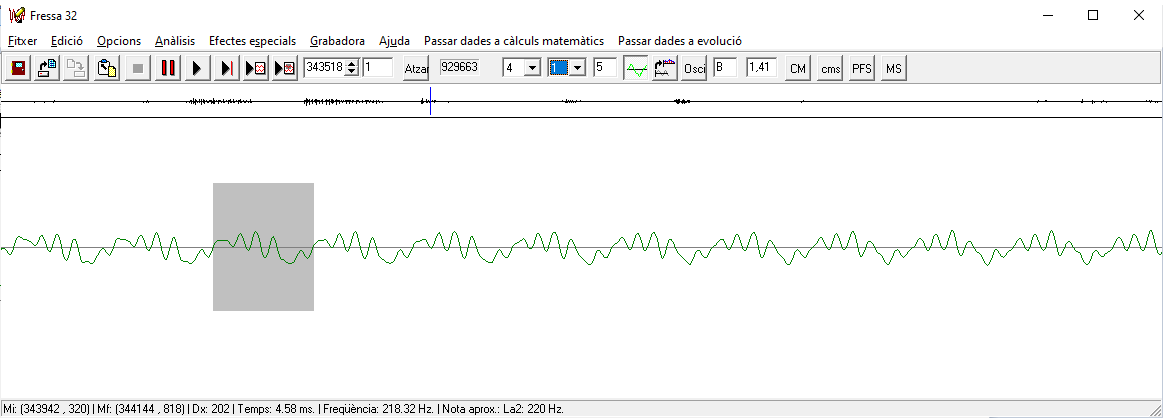 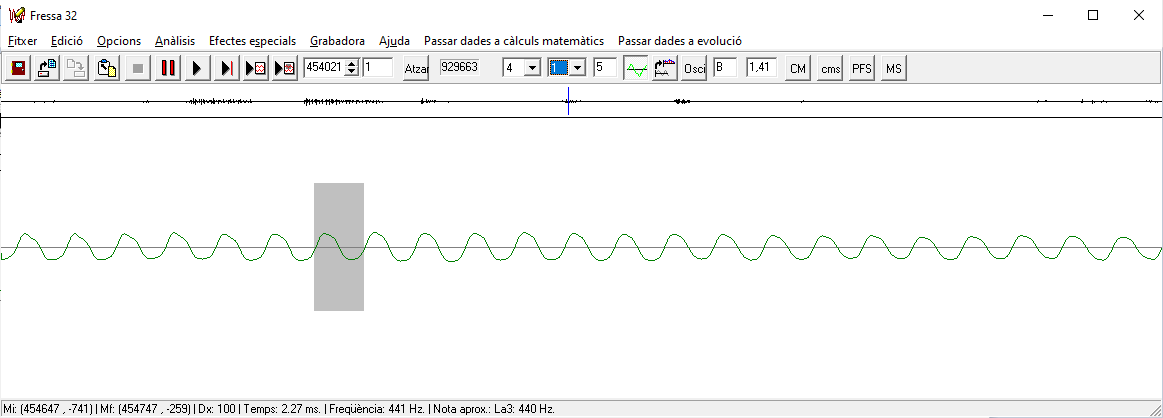 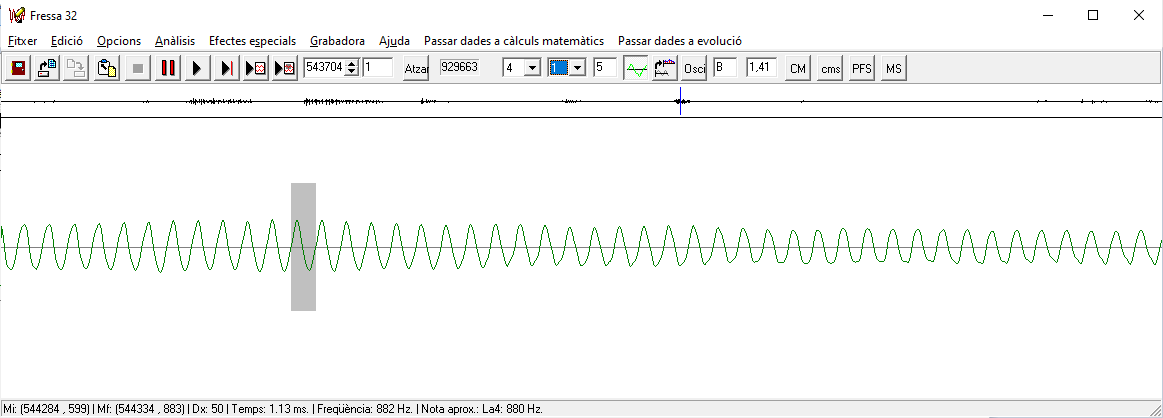 Si posem aquests números en una taula: 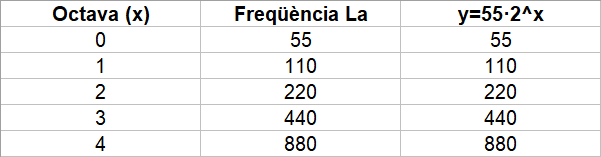 2-Però la cosa no s'acaba aquí.  Si mirem una única octava, veurem que hi ha 12 notes per passar d'una a l'altra. Contant notes i semitons (sostinguts). I si volguéssim saber quan val la freqüència de cada nota hauríem de trobar per quin número hem de multiplicar la freqüència de cada nota per saber la freqüència de la nota següent. Com ho podem fer? Nosaltres sabem que de `La` al `La` següent, la freqüència es multiplica per `2`. Com que hem de multiplicar 12 vegades, ja que hi ha 12 semitons entre `La` i `La` `=>` `x^12=440/220` `x^12=2` `x=x^(1/12)=root(12){2}` Així per saber com trobar quina és la freqüència d'una nota, de l'octava central del piano, hem de fer sevir aquesta fórmula: Per exemple si volem saber la freqüència del `sol`, només cal contar quant de semitons hi ha entre el La (220 hz) i el `sol`: `8` semitons.  3-Però la cosa de les exponencials en la música tampoc s'acaba aquí i encara es torna més surrealista. El fet de conèixer totes aquestes coses fa que ja ni necessitem instruments musicals per fer música. Escolta: L'instrument que fa la melodia, NO ha existit mai. Ha estat generat per operacions amb funcions matemàtiques, entre elles una exponencial negativa. Es calculen tot un seguit de números que en ser enviats a un altaveu fan que escoltem, el que estem escoltant ;-). La fórmula. Guaita que fan ara. Torna a sortir les funcions trigonomètriques del tema anterior. La gràfica d'aquest so, s'assembla a: 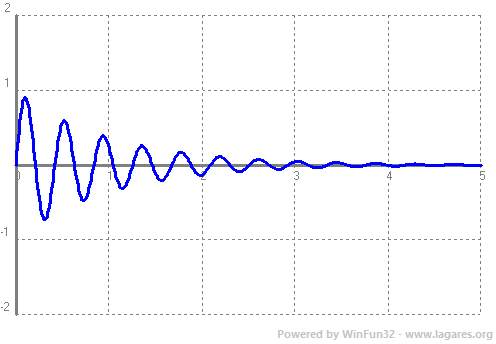 Si algú està interessat a aprofundir en aquest tema, us faig saber que tot això és possible gràcies a un projecte anomenat, Música, Física y Matemáticas, creat l'any 1996. En el link anterior podeu baixar el programa que permet sintetitzar sons a partir de fórmules matemàtiques. Aquí, hi ha un lloc on s'explica el perquè de tot plegat. 4-No se vayan todavía, aún hay más!!! Si agafem el període de l'ona de cada `La`, 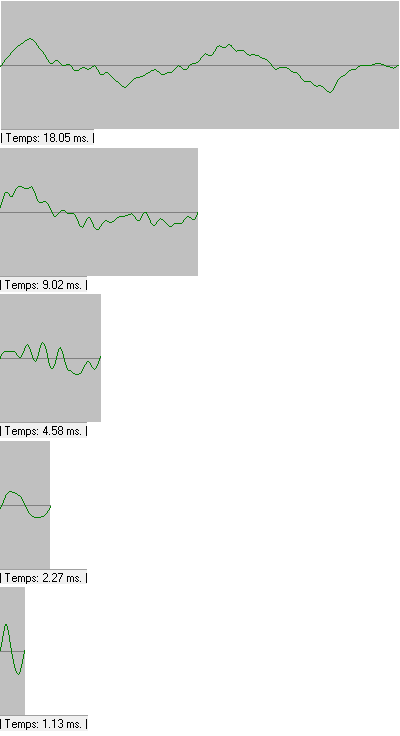 Observem que cada un (període), és la meitat de l'anterior. 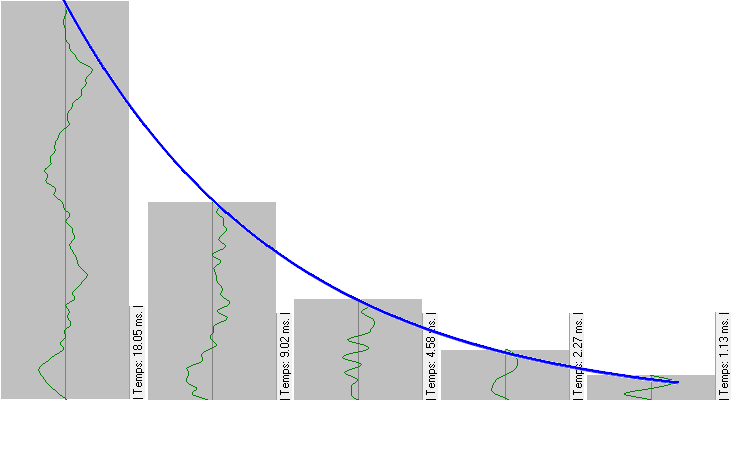 Això és una exponencial amb base, `(1/2)`, més petita que `1`. La qual cosa suposa funció decreixent tal com hem vist més amunt. Si recordem que `a^(-x)=(1/a)^x`. La fórmula anterior la podem posar: 5-I en aquest joc musical d'exponencials, no podíem oblidar el dibuix ideat pel vostre excompany d'institut, Aniol Puell, sobre les figures musicals. És la il·lustració de l'índex del tema.  - Agafa la taula de l'exercici anterior, la que relacionava la octava amb la freqüència i fes una nova taula on a la `x` hi poses la `y` de la primera taula i a la `y` hi calcules el `log_2(x/55)`. Què obtens? 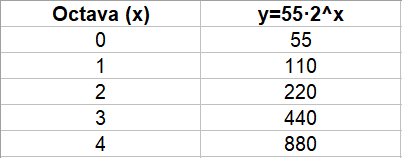 SOLUCIÓ:  - Mirant els dos problemes anteriors veiem que la funció exponencial i la logarítmica estan d'alguna manera relacionades. a) En el programa funcions i en una mateixa pantalla dibuixa `f(x) = 2^x` i `g(x) = log_2(x)`. Què observes? 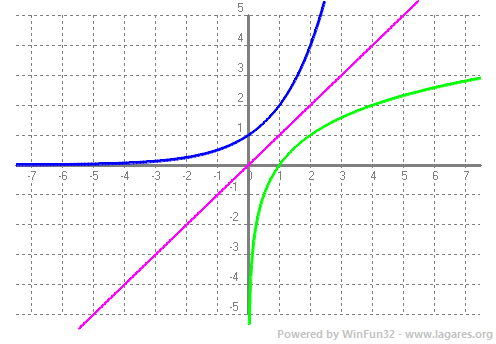 b) Fes el mateix que en l'apartat a `f(x) = 10^x` i `g(x) = log(x)`. Què observes? 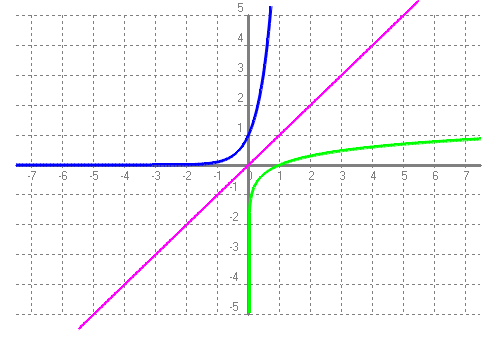 c) Quan passa el que acabes d'observar, quina relació diem que tenen les dues funcions una respecte l'altra?
Que són simètriques respecte la bisectriu del primer quadrant. La recta `y=x` d) Dibuixa la següent composició de funcions `log_2 2^x`. 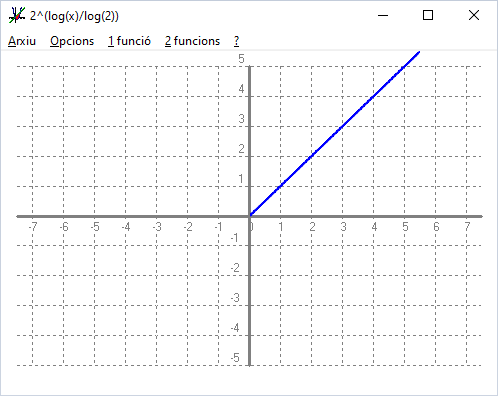 e) Dibuixa la següent composició de funcions `log 10^x`. 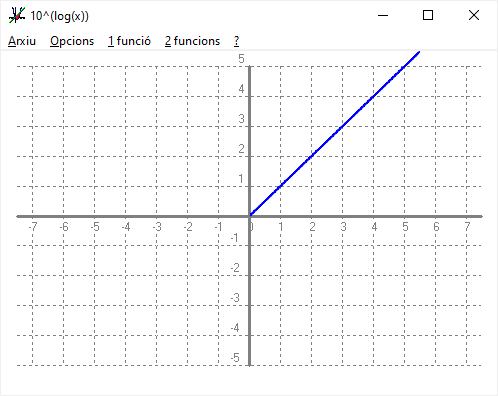
Quan composem dues funcions i dona la funció identitat, `y=x` diem que una és inversa de l'altra. Aixó la funció, `log_2 x` és al funció inversa de la funció, `2^x` i la funció, `log x`, és la funció inversa de `10^x`. I gràficament són simètriques respecte la bisectriu del primer quadrant. - Calcula el valor de la incògnita x en les igualtats següents.
b) `log_x 36=2` c) `log x = 5` d) `log_x 5^3 = -3` e) `log_5 x=4` SOLUCIÓ: - Desenvolupa les expressions següents fent servir logaritmes en base 10 utilitzant les propietats de les operacions amb logaritmes (exercici 16).
b) `e = a/(b^3 · c^5)` c) `e = (a · b^(-2) · c^2)^3/(d^(-2) · f^3)` SOLUCIÓ: L'apartat c, al final, té un fallo. `3·2log c` ha de ser `6log c` en lloc de `3log c`. Per la qual cosa el resultat final correcte és: - Si log 3 = t, escriu els següents logaritmes en funció de t.
b) `log 2700` c) `log (1/81)` d) `log 0'03` e) `log ((0'9)/(7'29))` f) `log (10^2/243)` SOLUCIÓ: - Resol les següents equacions. Se'n diuen equacions exponencials perquè la x està a l'exponent. La forma de resoldre-ho és tractar de posar a cada costat dues potències amb la mateixa base. Si les bases són diferents caldrà posar logaritmes a cada costat.
b) `8^(2x+3) = 4^x` c) `3^x = 30` d) `2^(x^2+1) = 32` e) `5^(2x) - 3 = 47` - Resol les següents equacions. Se'n diuen equacions logarítmiques perquè la x està afectada per un logaritme. La forma de resoldre-ho és tractar de posar a cada costat dos logaritmes amb la mateixa base.
Nota: S'ha canviat perquè doni un resultat que faci l'exercici més entenedor. b) `log_2 x + log_2 (x - 2) = 3` c) `log_2 x^2 - log_2 (x - 3/4) = 2` d) `2 log x - 4 log 2 = 3 log x` SOLUCIÓ:
f) `ln 2 + ln(11 - x^2) = 2 ln(5 - x)` g) `3 log_2 x - 2 log_2 (x/3) = 2 log_2 3 + 1` SOLUCIÓ: - Si mai necessites comprar una cosa, per exemple una casa, i no tens prou diners pots anar a una entitat financera (un banc per exemple) que et facin un préstec. El que es pacta és: D, els diners que et deixen, i la taxa d'interés anual que cobrarà el banc pel servei, el temps, t, normalment anys, que s'anirà tornant els diners més els interessos. Si es fa un pagament cada any, s'anomena anualitat d'amortització a la quantitat que cal pagar al banc cada vegada de manera que al cap dels t anys que s'ha pactat es saldi tot el deute. Per calcular aquesta anualitat el professor t'explicarà com fer-ho o bé pots veure el següent vídeo: Al final del vídeo s'explica que no cal fer tot el procés de calcular l'anualitat d'amortització per aproximacions successives. Es pot calcular mitjançant la fórmula: 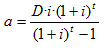 a) Fes un full de càlcul amb el Google Docs on hi hagi la taula d'amortització d'un préstec de 175000€ a tornar en 15 anys al 4% d'interés anual. Suma totes les quantitats abonades al banc i també els interessos que ha cobrat pel servei. Comparteix-lo amb el teu professor. b) Normalment no es van tornant els diners d'un préstec cada any. S'acostuma a pagar un a quantitat cada mes anomenada mensualitat d'amortització. La fórmula per calcular cada mensualitat és la següent: (f és la freqüència en que es paga cada any. Així si es paga cada mes, f = 12) 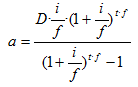 Fes un nou full de càlcul amb una taula d'amortització pel mateix capital anterior i en les mateixes condicions, però ara pagant cada mes en lloc de cada any. Suma totes les quantitats abonades al banc i també els interessos que ha cobrat pel servei. Comparteix-lo amb el teu professor. Nota: En ambdós casos: Si en lloc de fer servir el full de càlcul del Google Docs ho fas en un full de càlcul convencional, Excel, OpenOffice Calc, etc. envia-lo per email al teu professor. |