|
Dibuixa les funcions anteriors amb el programa funcions i indica, en cas de que en tingui: 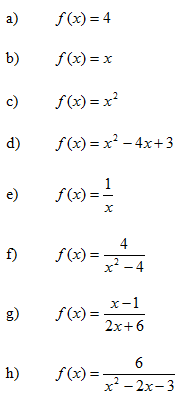
Per qüestions de completitud hi afegim el domini calculat en el problema anterior. a) 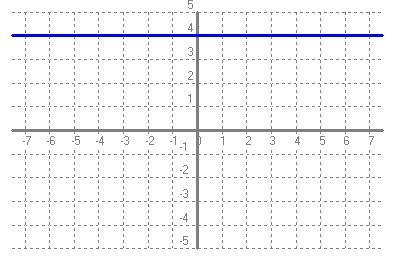
Recorregut: {4} Arrels: No en té Ordenada a l'origen: 4 Asímptotes verticals: No en té Asímptotes horitzontals: No en té Punts de discontinuïtat: No en té Intervals de creixement: No en té Intervas de decreixement: No en té Màxims: No en té Mínims: No en té b) 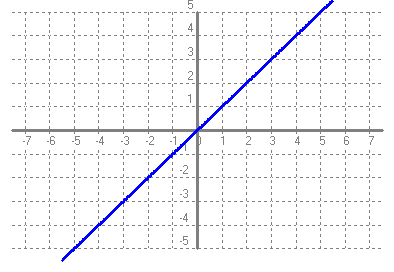
Recorregut: R Arrels: 0 Ordenada a l'origen: 0 Asímptotes verticals: No en té Asímptotes horitzontals: No en té Punts de discontinuïtat: No en té Intervals de creixement: (-∞ , +∞) Intervas de decreixement: No en té Màxims: No en té Mínims: No en té c) 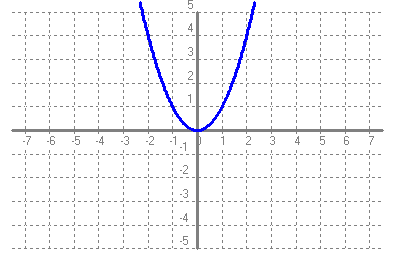
Recorregut: (0 , +∞) Arrels: {0} Ordenada a l'origen: 0 Asímptotes verticals: No en té Asímptotes horitzontals: No en té Punts de discontinuïtat: No en té Intervals de creixement: (0 , +∞) Intervas de decreixement: (-∞ , 0) Màxims: No en té Mínims: Punt (0 , 0) d) 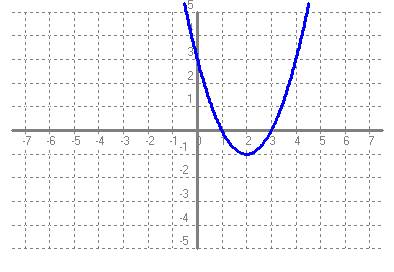
Recorregut: (-1 , +∞) Arrels: {1 , 3} Ordenada a l'origen: 3 Asímptotes verticals: No en té Asímptotes horitzontals: No en té Punts de discontinuïtat: No en té Intervals de creixement: (2 , +∞) Intervas de decreixement: (-∞ , 2) Màxims: No en té Mínims: Punt (2 , -1) e) 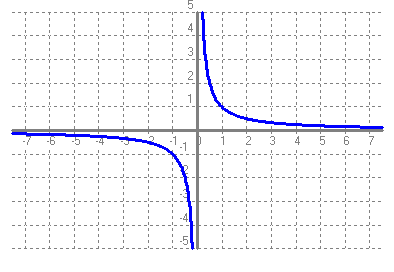
Recorregut: R - {0} Arrels: No en té Ordenada a l'origen: No en té Asímptotes verticals: x = 0 Asímptotes horitzontals: y = 0 Punts de discontinuïtat: x = 0 Intervals de creixement: No en té Intervas de decreixement: (-∞ , 0) ∪ (0 , +∞) Màxims: No en té Mínims: No en té f) 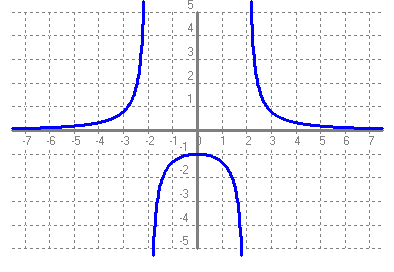
Recorregut: (-∞ , -1] ∪ (0 , +∞) Arrels: No en té Ordenada a l'origen: {-1} Asímptotes verticals: x = -2 i x = 2 Asímptotes horitzontals: y = 0 Punts de discontinuïtat: x = {-2 , 2} Intervals de creixement: (-∞ , -2) ∪ (-2 , 0) Intervas de decreixement: (0 , 2) ∪ (2 , +∞) Màxims: Punt (0 , -1) Mínims: No en té g) 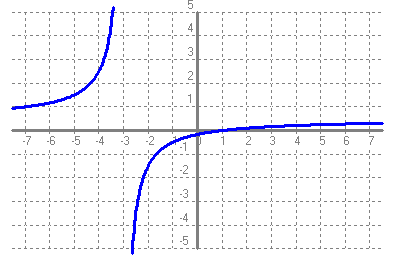
Recorregut: (-∞ , 0'5) ∪ (0'5 , +∞) Arrels: {1} Ordenada a l'origen:  Asímptotes verticals: x = -3 Asímptotes horitzontals: y = 0'5 Punts de discontinuïtat: x = {-3} Intervals de creixement: (-∞ , -3) ∪ (-3 , +∞) Intervas de decreixement: No en té Màxims: No en té Mínims: No en té h) 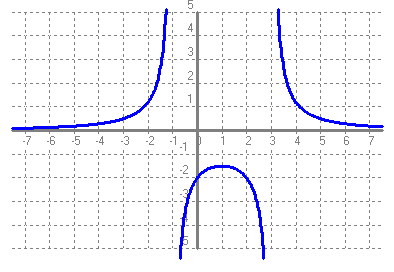
Recorregut: (-∞ , -1'5] ∪ (0 , +∞) Arrels: No en té Ordenada a l'origen: {-2} Asímptotes verticals: x = -1 i x = 3 Asímptotes horitzontals: y = 0 Punts de discontinuïtat: x = {-1 , 3} Intervals de creixement: (-∞ , -1) ∪ (-1 , 1) Intervas de decreixement: (1 , 3) ∪ (3 , +∞) Màxims: Punt (1 , -1'5) Mínims: No en té |