|
- Divideix els següents monomis: 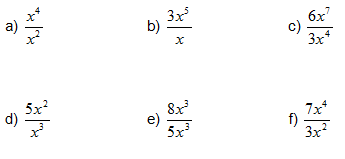
- Divideix 3x3 - 4x2 + 2x - 1 entre x2 - 1. Comprova el resultat amb la propietat, Divident = divisor · quocient + residu. - Divideix els següents polinomis:
b| (4x5 + 2x3 + 6x2 + 8x + 3) / 2x c| (5x5 - 3x4 - 2x3 + 6x2 + 5x + 2) / (x - 2) d| (4x6 + 2x5 - 3x4 + 7x2 - 2x - 8) / (x2 + 2x) e| (x6 + 4x5 - 4x3 + 3x2 + 3x + 6) / (x2 - 2x + 3) f| (6x5 - 12x4 - 16x3 + 14x2 + 12x - 3) / (3x2 - 2) - Divideix els següents polinomis fent servir la regla de Ruffini:
b| (4x5 + 2x3 + 6x2 - 8x + 3) / (x + 2) c| (5x5 - 3x4 - 2x3 + 6x2 + 5x + 2) / (x - 1) d| (4x6 - 19x5 + 14x4 - 13x3 + 21x2 - 9x + 18) / (x - 4) e| (x6 + 4x5 - 4x3 + 3x2 + 3x + 6) / (x + 1) - Calcula el valor numèric del polinomi P(x) pel número a que et donin. A continuació divideix el polinomi P(x) per (x - a):
b| P(x) = 2x2 - 3x + 2 i a = -2 c| P(x) = -3x3 + x2 - 4x + 2 i a = 3 d| P(x) = -x4 + 2x3 - 3x2 - 2x - 3 i a = 2 e| P(x) = 5x7 - 10 i a = 2 f| P(x) = x2 + 3x - 5/2 i a = 1/2 (o 0'5) - Calcula el valor de k del polinomi x2 - 3x + k de manera que si el dividim per (x - 4) el resultat és exacte. Fes-ho de dues maneres diferents. - Calcula el valor de k del polinomi x2 + kx - 6 sabent que si el dividim per (x + 2) el residu dóna 0. Fes-ho de dues maneres diferents. - Calcula el valor de k del polinomi x3 + kx2 + 3x - 2 sabent que si el dividim per (x - 2) el residu dóna 3. Fes-ho de dues maneres diferents. - Calcula:
b| (x-3)2 c| (x-2)·(x+2)·x d| (x-1)2·(x-3)·3x e| (x2+1)·x2·(x-3) f| (x2+2x+2)·(x+3)·x3 - Factoritza els següents polinomis:
b| x2-5x+4 c| x4-2x3-3x2 d| x2+x+1 e| x3+4x2+x-6 f| x4+2x3+3x2 g| 3x2+15x+12 h| 2x5+6x4-10x3-30x2+8x+24 - Escriu tres polinomis un de grau 2, un de grau 4 i l'altre de grau 5 i fes-ne la seva descomposició. Per fer-ho pots decidir quines arrels tindran i llavors construir el polinomi multiplicant. Per exemple x·(x-2)2·(x+1)·(x+3). - Digues si amb els següents parells de polinomis hi ha relació de divisibilitat, o sigui si el primer és divisor del segon:
b| P(x) = x-2 i Q(x) = x2+x-6 c| P(x) = x-6 i Q(x) = x2+x-6 d| P(x) = x2-4 i Q(x) = (x-2)·(x+2) e| P(x) = x2-5x+6 i Q(x) = x3-4x2+x+6 - Troba el Màxim Comú Divisor i el mínim comú múltiple de:
b| P(x) = x2-x i Q(x) = x2-1 c| P(x) = x i Q(x) = x+2 d| P(x) = x2+x-6 i Q(x) = x2-3x+2 e| P(x) = x4+x3-4x2-4x i Q(x) = x3-4x2+x+6 - Simplifica les següents fraccions algebraiques: 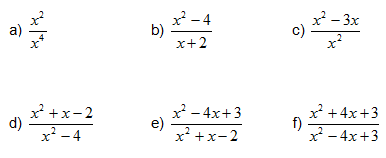
- Calcula les següents operacions amb fraccions algebraiques: 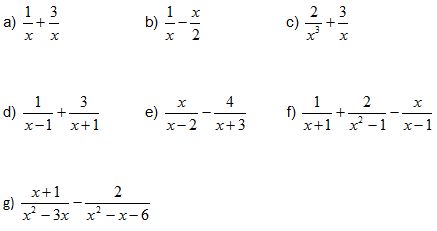
- Calcula (i simplifica, si es pot) les següents operacions amb fraccions algebraiques: 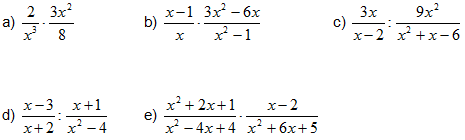
- Calcula (i simplifica, si es pot): 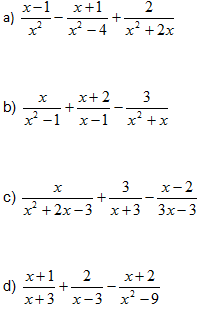
- Calcula (i simplifica, si es pot): 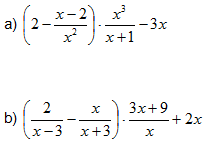
|