|
Fent servir el que has après en els exercicis anteriors, series capaç de trobar la fórmula de les funcions de l'exercici 3. Totes les formes de les gràfiques són iguals que y = x2, per la qual cosa l'únic que hem de mirar és on hi ha el vèrtex i si les "banyes" van amunt o avall. Si el vètex és (p, q) i les "banyes" van amunt, l'equació de la paràbola és f(x) = (x-p)2 + q i si les "banyes" van avall, l'equació de la paràbola és f(x) = -(x-p)2 + q a) 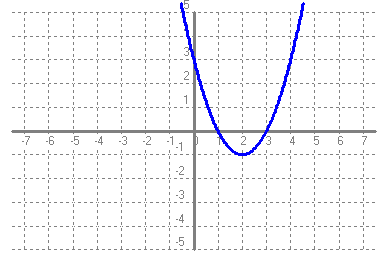 Vèrtex = (2, -1) Banyes = amunt f(x) = (x-2)2 - 1 = x^2 - 4x + 4 - 1 = x2 - 4x + 3 b) 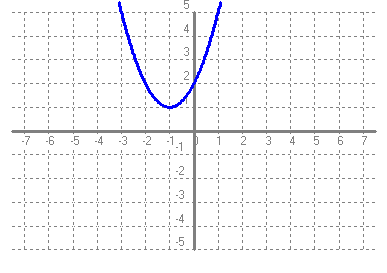 Vèrtex = (-1, 1) Banyes = amunt g(x) = (x+1)2 + 1 = x2 + 2x + 1 + 1 = x2 + 2x + 2 c) 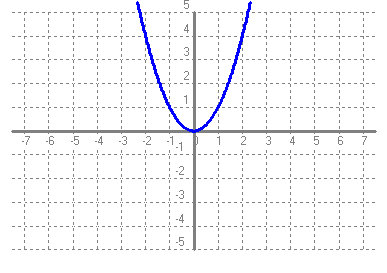 Vèrtex = (0, 0) Banyes = amunt h(x) = (x+0)2 + 0 = x2 d) 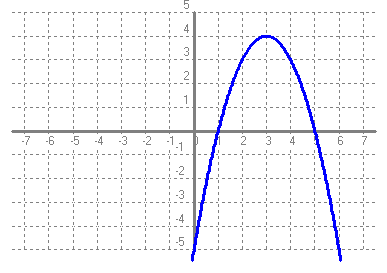 Vèrtex = (3, 4) Banyes = avall k(x) = -(x-3)2 + 4 = -(x2 - 6x + 9) + 4 = -x2 + 6x - 9 + 4 = -x2 + 6x - 5 |