MATEMÀTIQUES II - Sèrie 2 Setembre 1994
(16/10/97) - Tornar a l'índexOpció A
1-A l'oficina central de Correus d'un cert país hi ha exposades les tarifes del servei de cartes, que són les següents: (4 p)
-Cartes fins a 20 g de pes: 17 pts.
-per cada 10 g o fracció de 10 g d'excés de pes, s'hi ha d'afegir 5 pts. més.
a) Escriviu la fórmula de la funció y=f(x) (on x representa el pes de cada carta i y el preu que hem de pagar per enviar-la), fins a 50 g.
b) Representeu gràficament la funció f. Indiqueu en quins punts del seu domini és discontínua i perquè.
2-Resoleu: (2 p)
-
| 1 2 -1| |x| | 3|
| 2 1 +2|.|y|=|-4|
| 4 -3 4| |z| | 2|
3-En una loteria de 1.000 bitllets es rifen un primer premi i un segon premi, que es treuen successivament d'una caixa que conté els 1.000 números. Els esdeveniments "el primer premi correspon al 345" i "el segon premi correspon al 608", són dependents o independents? Raoneu la resposta. (2 p)
4-Abans de tirar una moneda perfecta 100 vegades fem les prediccions que el nombre de cares estarà entre:
a) [50-5, 50+5]
b) [50-7, 50+7]
Calculeu els riscs o probabilitats que la predicció falli en el cas a) i en el cas b) respectivament. Comenteu els resultats. (2 p)
Opció B
1-En unes proves d'alcoholèmia semblants a les que fa la DGT s'ha observat que el 5% dels conductors aturats donen positiu a la prova i que un 10% dels conductors aturats no duen cordat el cinturó de seguretat. També s'ha observat que les dues observacions són independents.
Un guàrdia de trànsit atura cinc conductors a l'atzar. Si tenim en compte que el nombre de conductors és prou gran per estimar que la proporció d'infractors no varia en fer la selecció,
a) determineu la probabilitat que exactament tres conductors hagin comès alguna de les dues infraccions.
b) determineu la probabilitat que almenys un dels conductors aturats hagi comès alguna de les dues infraccions. (4 p)
2-Determineu, mitjançant inequacions lineals, la regió del pla següent: (2 p)
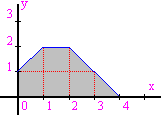
3-Calculeu per a quin valor de a la matriu següent no té inversa: (2 p)
| 1 | 2 |
| -1 | a |
4-Demostreu que la funció f(x)=1/x és decreixent en tot el seu domini (2 p)