1.4 ÀLGEBRA - PROGRAMACIÓ LINEAL
(12/10/97) - Tornar a l'índex - Baixar programari1.4.1-(1992/1/B) Considerem el conjunt de punts que satisfan les condicions:
x ³ 0, y ³ 0, x+2y ³ 7, 4x+3y ³ 18
Té mínim la funció z=3x+y en aquest conjunt? I màxim? Per què? (2 p).
1.4.2-(1992/3/A) Dibuixeu la zona del pla determinada per les condicions següents:
x ³ 0, y ³ 0, x+y £ 5, 2x+3y ³ 6
Pertany el punt (4,2) a la regió considerada? (2 p)
1.4.3-(1992/4/A) Calculeu el màxim de la funció z=x+y en el conjunt de punts que compleixen:
x ³ 0, y ³ 0, x+y £ 5, 4x+y £ 8
1.4.4-(1992/4/B) Dibuixeu la regió determinada per les condicions següents:
x ³ 0, y ³ 0, 2x+3y £ 18, 2x+y £ 10, x+3y ³ 3
Pertany el punt (3,2) a aquesta regió? (2 p)
1.4.5-(1992/5/B) Busquem el màxim i el mínim de la funció z=x+y, sotmesa a les restriccions següents:
x ³ 0, y ³ 0, 2x+y ³ 1, x+2y £ 4
1.4.6-(1993/2/A) Maximitzeu la funció z=3x-y amb les restriccions següents:
X+Y ³ 2 X £ 2 -X+Y £ 2 X ³ 0 Y ³ 0
1.4.7-(1993/3/A) Calculeu el valor màxim de la funció z=3x+y que es troba sotmesa a les restriccions següents:
x ³ 0, y ³ 0, y £ 3, x-y £ 1,2x+3y £ 12.
1.4.8-(1993/3/B) Trobeu la regió del pla sotmesa a les condicions següents:
x ³ 0, y ³ 0 x+y ³ 5, x+y ³ 8
Podem trobar el màxim i el mínim de la funció z=(1/2)x+y en aquesta regió? Raoneu la resposta.
1.4.9-(1993/4/B) Resoleu el sistema següent:
3x-1>4
2x+2<7
Indiqueu també quins dels valors de x següents són solucions del sistema i quins no: x=1, x=2, x=3.
1.4.10-(1993/5/B) Optimitzeu la funció z=3x+2y amb les restriccions següents:
x ³ 0, y ³ 0, 2x+y ³ 2, 4x+5y £ 20
1.4.11-(1994/2/B/Setembre) Determineu, mitjançant inequacions lineals, la regió del pla següent: (2 p)
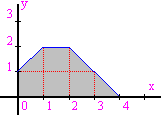
1.4.12-(1994/4/B) Dibuixeu la regió del pla formada pels punts que verifiquin:
-x+y<4
x+y<1
y<2
x<0, y>0
Indiqueu tots els vèrtex d'aquesta regió. (2 p.)
1.4.13-(1994/5/B) Determineu la regió del pla limitada per: (2 p.)
x+y>1
x<1
y<1
1.4.14-(1995/4/B) Escriu les inequacions que defineixen la regió del pla limitada pel quadrilàter de vèrtexs consecutius (0,1), (1,2), (3,2) i (2,0). (2 p)
1.4.15-(1995/2/B) Donat el sistema d’inequacions que segueix:
x+y ³ 2
x+y £ 4
y £ 2
x-y £ 2
representeu gràficament la regió factible i determineu-ne tots els vèrtex. (2 p)
1.4.16-(1995/6/A) Dibuixeu la regió del pla determinada per:
x+2y ³ 4
-x+y £ 2
2x+y £ 5
Pertany a aquesta regió el punt (2,2)? Raoneu la resposta. (2 p)
1.4.17-(1995/6/B) Calculeu el valor màxim de la funció z = x + 3y amb les restriccions: (2 p)
x+2y ³ 4
x+y £ 3
y £ 2
1.4.18-(1996/1/B) Indiqueu amb un sistema d'inequacions la regió del pla limitada pel triangle de vèrtex (1,1), (2,3), (3,1). (2p)
1.4.19-(1997/6/A/4/Juny) Dibuixeu la regió R del pla formada pels punts (x,y) que compleixen les dues desigualtats: 3x+2y ³ 1, x+y ³ 1. Busqueu després el mínim de la funció z = 3x + 2y en aquesta regió. Comproveu que el punt de coordenades x = 0,
y = 2 està situat a la regió R i que el valor que pren la funció en aquest punt és més gran que el valor mínim que heu calculat abans per a aquesta funció. (2 p)
1.4.20-(1997/3/B/4/Setembre) Dibuixeu la regió definida per les inequacions següents i calculeu-ne l'àrea: x + y ³ 8, y- x £ 5, x £ 4. (2 p)