2.2.19-(1995/4/A) Suposem que pòdem modelitzar la relació entre la temperatura de l'aigua de mar i la fondària en una zona determinada mitjançant la funció:
f(x)=(x²+4x+1)/(x²+1)
on x representa la fondària en metres negatius (p. ej.: -4,5 m) i f(x) la temperatura corresponent.
a) Indiqueu quina és la temperatura de l'aigua en superfície i a quines profunditats la temperatura és de 0 graus. Com evoluciona la temperatura de l'aigua a mesura que anem baixant?
b) Indiqueu a quina fondària la temperatura és més baixa i quina és aquesta temperatura. (4 p)
a.1-La temperatura en superfície és calcula mitjançant la imatge del 0f(0) = 1
a.2-Les profunditats que es troben a 0 graus són les antiimatges del 0 o sigui les arrels, les trobem igualan la funció a 0 i resolen la equació.
0 = (x²+4x+1)/(x²+1) => x²+4x+1 = 0
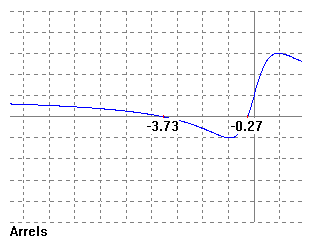
Resolem aquesta equació de segon grau -3'74 i -0'26.
O sigui a 374 i a 26 cm per sota la superfície la temperatura del aigua és de 0 graus.
a.3-Per saber com evoluciona hem de calcular el límit quan x tendeix a -infinit. Com es tracta d'un quocient de polinomis del mateix grau, aquest límit és el quocient de quoeficients que és 1.
O sigui a la llarga, a mesura que anem baixant la temperatura tendeix a estabilitzar-se a 1 grau.
b-Per trobar la temperatura mínima hem de buscar el mínim de la funció. Per fer-ho calcularem la funció derivada:
f'(x) = (-4x²+4)/(x²+1)²
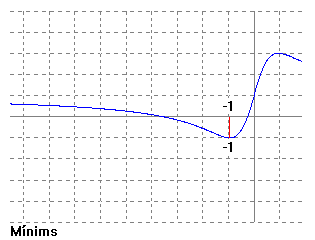
Que té dos zeros a 1 i a -1. Com només estudiem els valors de la x negatius ens quedem amb x = -1. Si busquem la seva imatge f(-1) = -1.
Com que té dos punts al seu voltant, -3'74 i -0'26, amb imatge 0 que és major que la imatge del -1, -1 veiem que és un mínim.
A un metre per sota la superfície la temperatura assoleix el mínim d'1 grau sota 0.