4.Dibuixeu la regió R del pla formada pels punts (x,y) que compleixen les dues desigualtats: 3x+2y ³ 1, x+y ³ 1. Busqueu després el mínim de la funció z = 3x + 2y en aquesta regió. Comproveu que el punt de coordenades x = 0, y = 2 està situat a la regió R i que el valor que pren la funció en aquest punt és més gran que el valor mínim que heu calculat abans per a aquesta funció. (2 p)
Cal dibuixar les rectes
3x+2y=1
x+y=1
i substituir per un punt de una de les regions en que queda separat el pla per veure si compleix o no la inequació. Si si és aquesta la regió, sinó l'altre.
La intersecció de les dues regions (per cada una de les dues inequacions) és la regió solució del sistema d'inequacions.
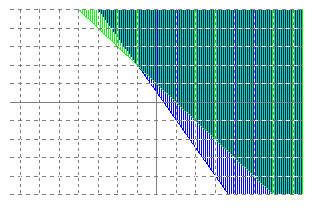
L'únic vèrtex de la regió és la intersecció de les dues rectes
3x+2y=1
x+y=1
què és el punt (-1,2) que té com a valor de la funció objectiu, z = 3x + 2y
z(-1,2) = 3(-1) + 2(2) = 1
Al ser una regió oberta això és un màxim o un mínim. Cerquem la imatge d'un altre punt de la regió, per exemple el que ens donen (0,2).
En primer lloc veiem que compleix el sistema d'inequacions.
3(0)+2(2) = 4 que és més gran que 1
(0)+(2) = 2 que és més gran que 1
Cerquem la imatge d'aquest punt (0,2) per la funció objectiu z = 3x + 2y
z(0,2) = 3(0) + 2(2) = 4
Veiem que la imatge de la funció objectiu d'aquest punt és més gran que la del vèrtex de la regió. Així dons aquest últim és un mínim.