
Vista de perfil de la secció
Si seccionem la superfície cònica amb un angle comprès entre l'horitzontal i la generatriu, obtenim una el·lipse.

Vista de perfil de la secció
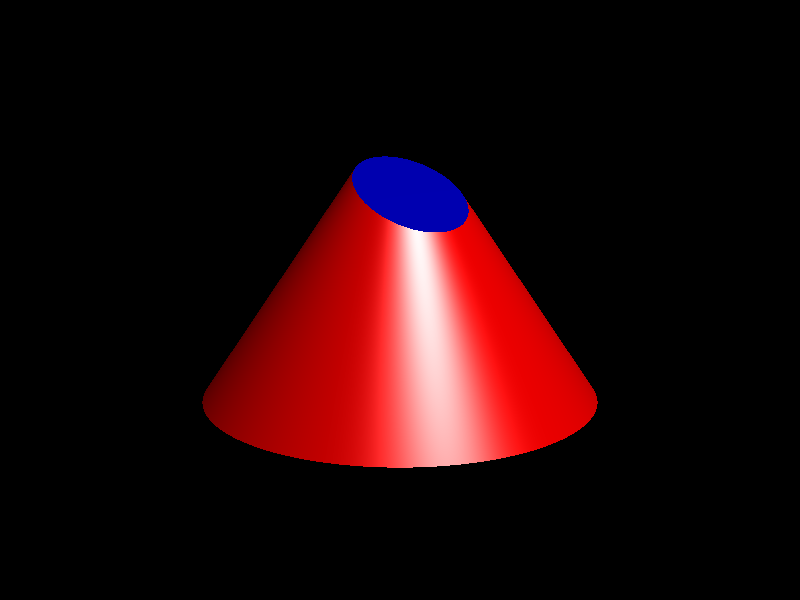
L'el·lipse
Dit d'una manera barroera, una el·lipse és com una circumferència aixafada. El paràmetre que descriu aquest aixafament s'anomena excentricitat, que pot prendre valors entre 0 i 1. Podem obtenir una el·lipse poc excèntrica si la secció és propera a l'horitzontal, i a mida que l'angle de secció augmenta, augmenta l'excentricitat.
 Excentricitat = 0,1 |
 Excentricitat = 0,2 |
 Excentricitat = 0,3 |
 Excentricitat = 0,4 |
 Excentricitat = 0,5 |
 Excentricitat = 0,6 |
 Excentricitat = 0,7 |
 Excentricitat = 0,8 |
 Excentricitat = 0,9 |
Els elements imprescindibles per a construir l'el·lipse són dos punts anomenats focus i una longitud, que ha de ser més gran que la distància focal. L'el·lipse és la corba formada pels punts tals que la suma de les distàncies als dos focus és constant.
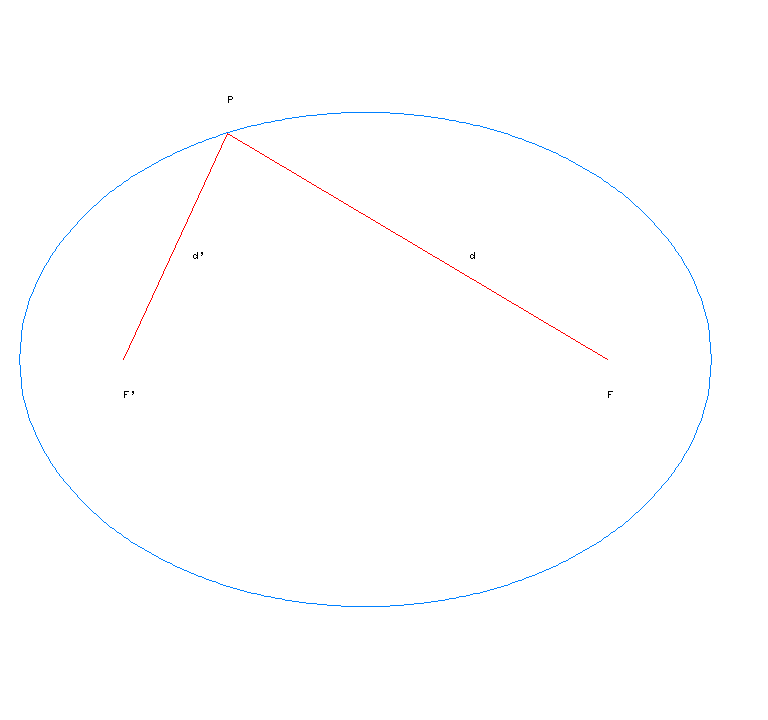
El·lipse = {P/d+d'=constant}
Si un raig surt d'un focus de l'el·lipse, no importa on vagi a reflectir-se de l'el·lipse, que segur que va a parar a l'altre focus.

Propietat reflectiva de l'el·lipse
Si seccionem la superfície cònica amb un angle igual al de i la generatriu, obtenim una paràbola.

Vista de perfil de la secció
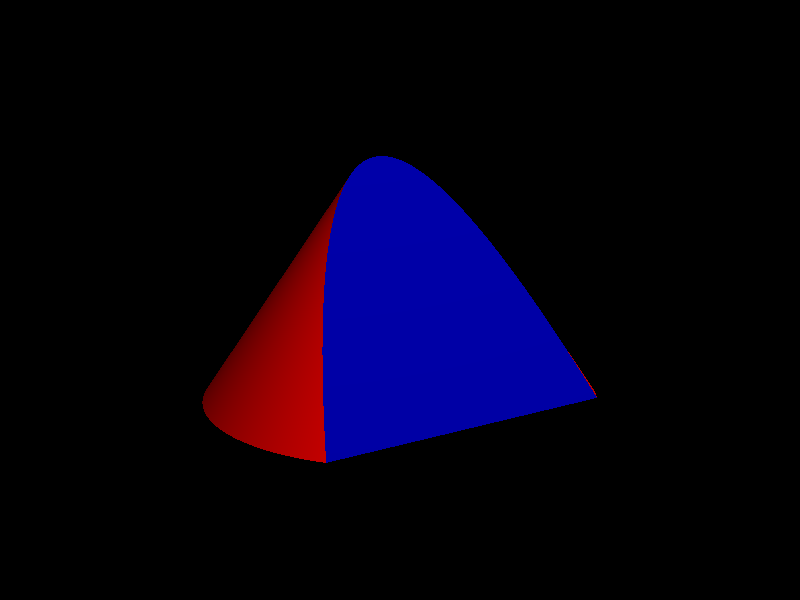
La paràbola
Els elements imprescindibles per a construir la paràbola són un punt anomenat focus i una recta anomenada directriu. La paràbola és la corba formada pels punts tals que la distància al focus és igual que la distància a la directriu.
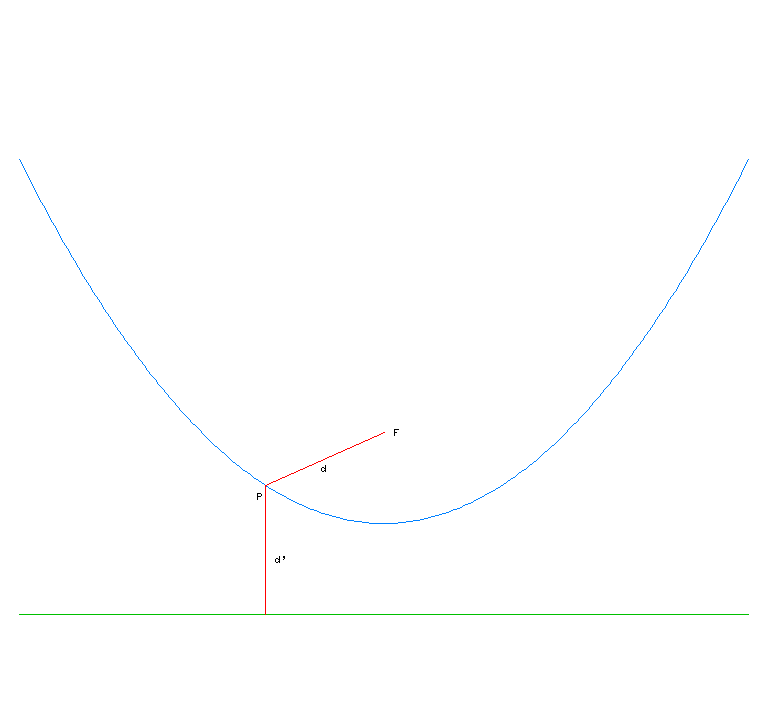
Paràbola = {P/d=d'}
Si un raig surt del focus de la paràbola, no importa on vagi a reflectir-se de la paràbola, que segur que surt paral·lel a l'eix de la paràbola.
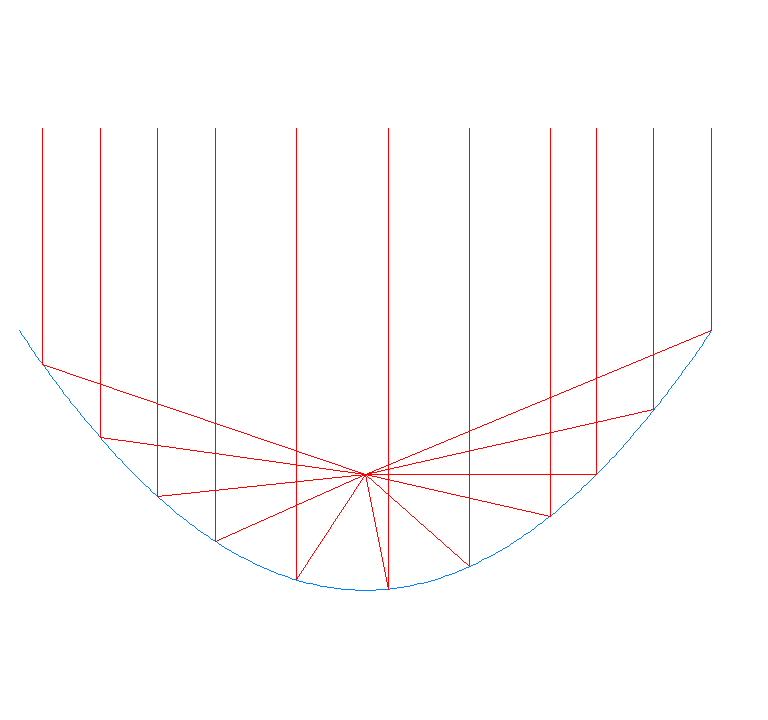
Propietat reflectiva de la paràbola
Si seccionem la superfície cònica amb un angle comprès entre la generatriu i la vertical, obtenim una hipèrbola.

Vista de perfil de la secció

La hipèrbola
L'obertura de les branques de la hipèrbola està regulada per un paràmetre anomenat excentricitat, que sempre pren valors més grans que 1.
 Excentricitat = 1,2 |
 Excentricitat = 1,5 |
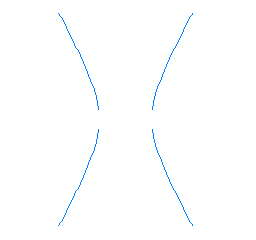 Excentricitat = 2 |
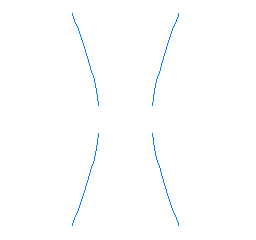 Excentricitat = 2,5 |
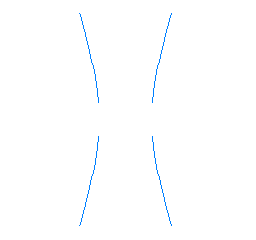 Excentricitat = 3 |
 Excentricitat = 4 |
Els elements imprescindibles per a construir una hipèrbola són dos punts anomenats focus i una longitud, que ha de ser més petita que la distància focal. La hipèrbola és la corba formada pels punts tals que la diferència de les distàncies als dos focus és constant.
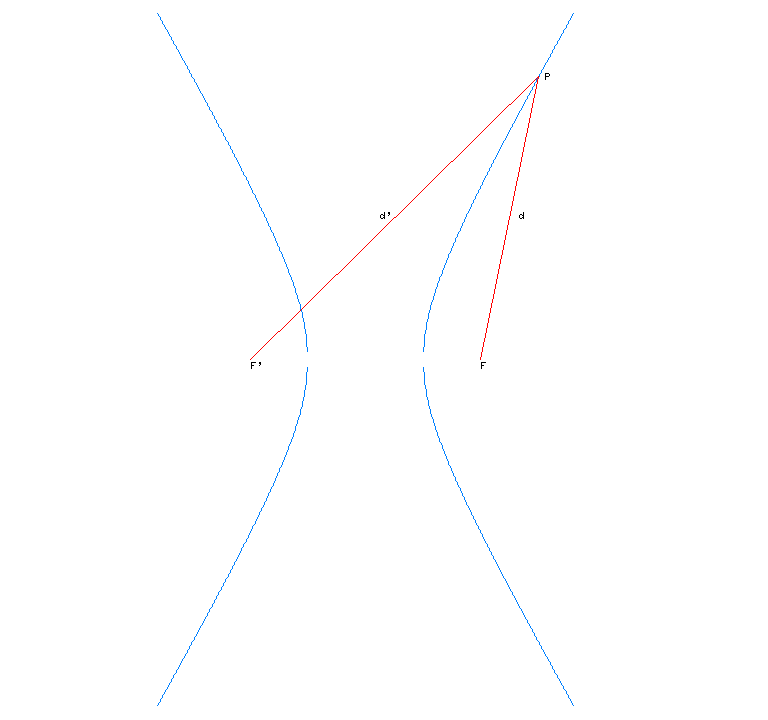
Hipèrbola = {P/|d-d'|=constant}
Si un raig surt d'un focus de la hipèrbola, surt reflectit com si provingués de l'altre focus.
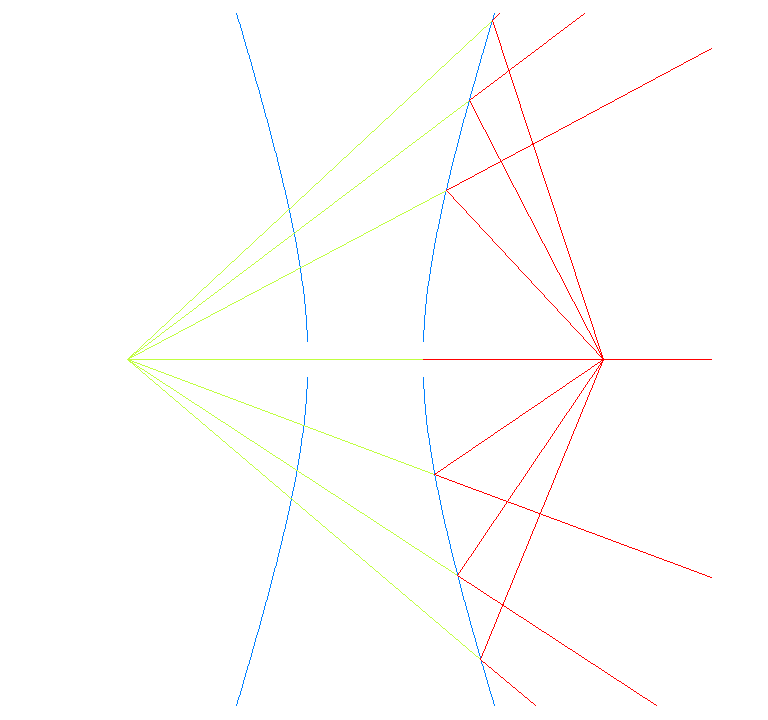
Propietat reflectiva de la hipèrbola
Aquesta web complementa les classes del tema de còniques de 1r de batxillerat del curs 2004-5.
Les imatges de les seccions còniques s'han creat amb el programa POVRAY. Les altres s'han creat amb el programa GnuPlot.