L'arc capaç
La punta de l'escaire
- Pren un full i dos claus petits o agulles de cap.
- Clava'ls en el full, deixant una separació d'uns quants centímetres. Millor si a sota hi tens una superfície semidura com un suro.
- Agafa un escaire de dibuix i fica un dels seus vèrtexs entre les dues agulles; fes una marca en el lloc abastat pel vèrtex.
- Ves provant altres orientacions de l'escaire per tal de tenir més marques.

|
Aquestes marques formen una figura coneguda. Quina és?
|
- Sobre el mateix full, i sense canviar de lloc els claus, fes el mateix amb l'altre vèrtex de l'escaire. Utilitza un altre color per fer les marques.
- Repeteix el mateix procés amb els vèrtexs d'un cartabó.
|
Quines figures van apareixent? Enuncia el resultat que acabes d'obtenir.
Quina relació hi ha entre el vèrtex emprat per fer les marques i la figura obtinguda?
Tots els punts que has trobat tenen una mateixa propietat: des de qualsevol punt d'aquest ......... , l'angle amb que es veuen les dues agulles és .........
|
Ara, amb el GeoGebra
- Crea dos punts i anomena'ls O i A.
- Fes una circumferència amb centre O i que passi pel punt A.
- Marca un altre punt sobre la circumferència. Anomena B aquest nou punt.
- Marca un altre punt sobre la circumferència, en la part on l'arc que uneix els punts A i B és major. Anomena C aquest nou punt.
- Fes els segments AC i BC.
- Determina l'angle ACB i mesura'l. Per ressaltar-los, canvia el color del punt C, dels segments AC i BC i de l'angle ACB.
- Mou el punt C. Quins valors pren l'angle ACB?
- Mou ara el punt B. Quins valors pren l'angle ACB?
- Sense fer els segments AO i BO, determina l'angle AOB i mesura'l.
|
Quin nom rep un angle com els AOB? (Pista: fixa't on té el vèrtex l'angle AOB)
Quin nom rep un angle com els ACB? (Pista: fixa't on té el vèrtex l'angle ACB)
Ves provant diferents posicions del punt B i anota els valors de l'angle ACB per a cada valor de l'angle AOB. Quina relació hi ha entre els angles AOB i ACB? Enuncia el resultat que has observat.
|
- Marca un altre punt sobre la circumferència, en la part on l'arc que uneix els punts A i B és menor. Anomena D aquest nou punt.
- Fes els segments AD i BD.
- Determina l'angle ADB i mesura'l. Per ressaltar-los, canvia el color del punt D, dels segments AD i BD i de l'angle ADB.
- Mou el punt D. Quins valors pren l'angle ADB?
- Mou ara el punt B. Quins valors pren l'angle ADB?
|
Per cada valor d'AOB, mesura els angles ACB i ADB. Pren vàries mesures d'aquests angles (mínim 15, millor 25), organitza'ls en una taula i fes les gràfiques que mostrin com depen ACB respecte AOB, com depen ADB respecte ACB i com depen ADB respecte AOB.

Quines relacions hi ha entre aquests angles? Enuncia el resultat que has observat.
|
Construcció inversa (sense GeoGebra)
- Dibuixa dos punts, que anomenaràs A i B (que representen els llocs on havies clavat les agulles).
- Fes el segment AB.
- Volem trobar l'arc que formaria un angle de 65 graus
|
On hauríem de situar el centre O? (Observa la forma del triangle OAB i les relacions entre els seus angles)
I si l'arc l'hagués format un angle de 80 graus?
I un de 40 graus?
I un de 20 graus?
|
Una aplicació
|
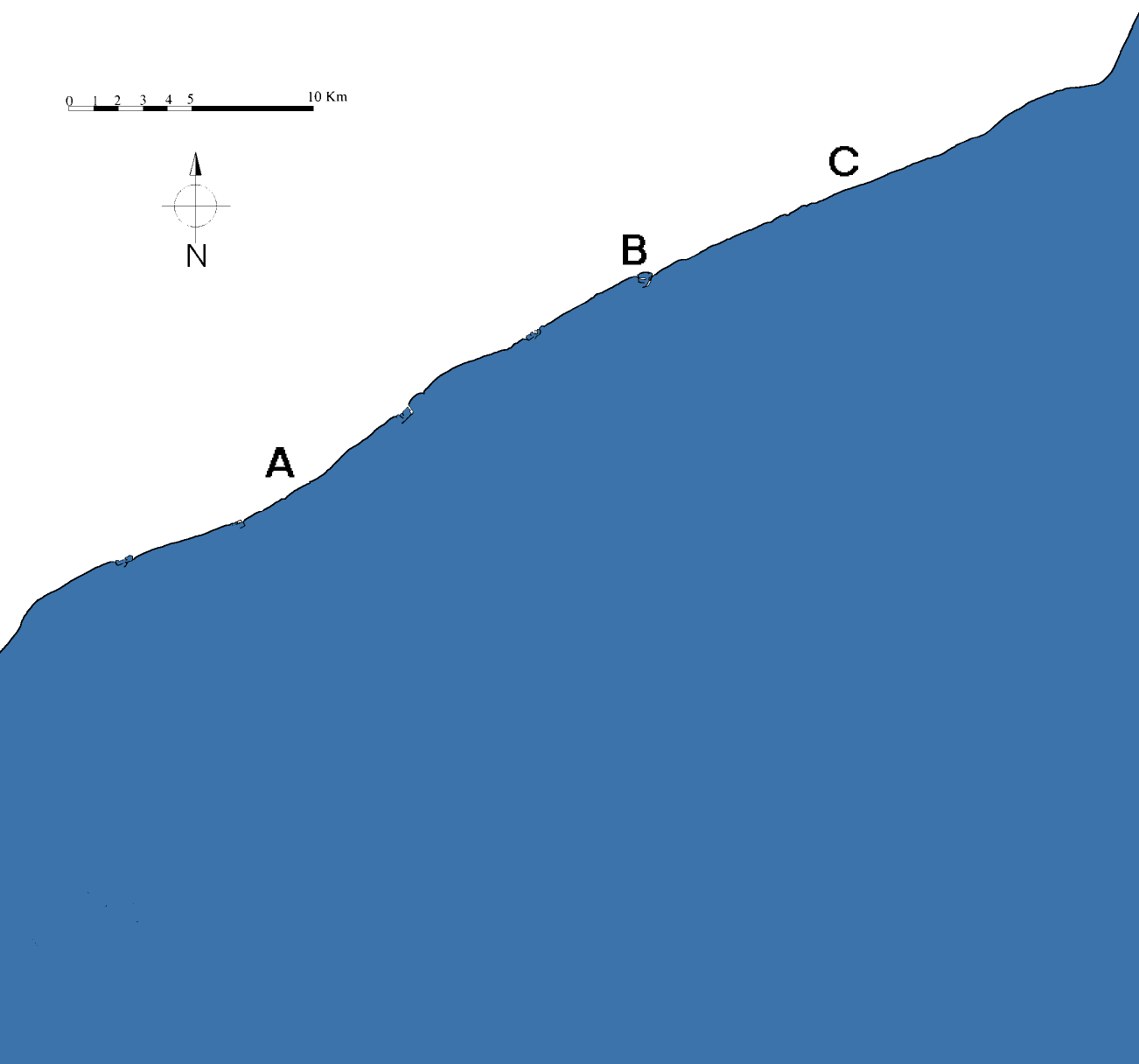
Un mariner ens diu que des d'on està la seva barca veu que l'angle entre la Torre d'en Nadal i el port d'Arenys és de 35 graus. És possible saber la seva posició només amb aquesta dada? Explica-ho.
La distància entre la Torre d'en Nadal i el port d'Arenys és d'uns 15 km.
|
|
Ara, el mateix mariner ens diu que veu que l'angle entre la Torre d'en Nadal i el port d'Arenys és de 35 graus i, alhora, que l'angle entre el port d'Arenys i el far de Calella és de 50 graus. És possible saber la seva posició només amb aquestes dades? Explica-ho.
La distància entre el port d'Arenys i el far de Calella és d'uns 9 km.
|
Per què passa això? (ampliació)
- Crea una circumferència amb centre O, i amb els punts A, B i C sobre la circumferència (recorda que C ha d'estar a l'arc major que formen A i B).
- Dibuixa el triangle OAC i pinta'l.
- Fixa't amb el triangle OAC. De quin tipus és? Com són els seus angles? Quina relació hi ha entre ells? Escriu-la.
- Dibuixa el triangle OBC i pinta'l. Situa el punt C de manera que els dos triangles no estiguin superposats.
- Fixa't amb el triangle OBC. De quin tipus és? Com són els seus angles? Quina relació hi ha entre ells? Escriu-la.
- Ara fixa't amb l'angle ACB. De quina manera es pot descomposar l'angle ACB en dos angles que hagin aparegut en els triangles OBC i OAC?
- I ara fixa't en l'angle AOB. Si coneguéssim els angles dels triangles AOC i AOB, com el podríem deduir?
|
Juntant totes aquestes relacions entre angles, què pots dir de la relació entre ACB i AOB?
|
- Comencem amb la circumferència amb centre O, i amb els punts A, B i D sobre la circumferència.
- Dibuixa el triangle OAD i pinta'l.
- Fixa't amb el triangle OAD. De quin tipus és? Com són els seus angles? Quina relació hi ha entre ells? Escriu-la.
- Dibuixa el triangle OBD i pinta'l.
- Fixa't amb el triangle OBD. De quin tipus és? Com són els seus angles? Quina relació hi ha entre ells? Escriu-la.
- Fixa't amb l'angle ADB. De quina manera es pot descomposar l'angle ADB en dos angles que hagin aparegut en els triangles OAD i OBD?
|
Quina relació hi ha entre els angles ADB i AOB?
|
|
I quina relació hi ha entre els angles ADB i ACB?
|
Tornar al llistat d'activitats
Tornar a la pàgina inicial
|