Som als vestidors de l'equip.
L'entrenador ens ha citat per a una classe teòrica. Vol que aprenguem a situar-nos en la millor posició en el camp per a marcar...
Nosaltres li hem dit que ja ho sabem, que no cal que ens ho mostri, però ell, que és molt cabut, insisteix.
Hi anem, no sigui que s'empipi i al pròxim partit no ens convoqui a jugar.
Comença parlant-nos de la posició en la frontal de l'àrea i compara la situació amb l'entrada pels extrems: vol que reflexionem referent a dues variables, a dos aspectes: l'angle de tir i la distància a la porteria.
En Lolo li ha replicat que això és una tonteria perquè tots sabem que la millor posició és la que quedi més a prop de la porteria.
És clar, com que el Lolo té el lloc assegurat a l'equip, s'atreveix a portar-li la contrària.
Però el Míster l'ha tallat en sec —molt ben fet, Míster, el Lolo és un savitites!— dient-li que la distància a la porteria no és l'única variable a tenir en compte, que s'ha de combinar amb l'angle de tir.
En Lolo s'ha quedat mut durant la resta de la sessió. Potser pensa que la teoria no és el que millor domina...
En fí, ens ha proposat un exercici que ens recordava el nostre pas —no de tots, és clar— per l'institut, quan estudiàvem coses poc útils i les havíem de comprendre i raonar. L'exercici és aquest...
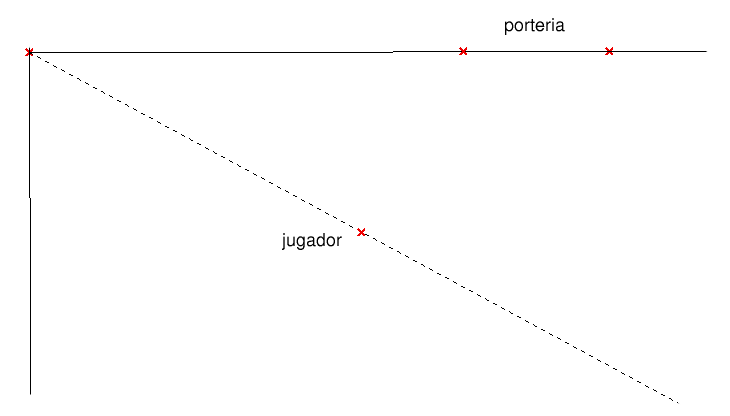
La situació que ens hem d'imaginar és la següent: un jugador surt corrents de l'extrem, del còrner, seguint una trajectòria rectilínia.
Anem a raonar les aventatges i els inconvenients de cada punt de xut.
