El teorema de Pitàgores
|
|
L'enunciat conegut com el teorema de Pitàgores diu que en tot triangle rectangle, la suma de les àrees dels quadrats construits sobre els catets és igual a l'àrea del quadrat construit sobre la hipotenusa (Euclides, llibre I, proposició 47): A vegades, l'enunciat invers (si en un triangle es verifica aquesta relació entre àrees, aleshores aquest triangle és rectangle, Euclides, llibre I, proposició 48) s'inclou també en el teorema. Què passa si el triangle no és rectangle?
Aquí hi ha una petita recopilació d'algunes demostracions visuals del teorema. S'han extret dels llibres Pitágoras de Pedro Miguel González Urbaneja (ed. Nívola, 2001) i The Pythagorean Theorem d'Eli Maor (Princeton Univ. Press, 2007). Fes la construcció del triangle rectangle amb els quadrats construits sobre els costats i la seva equivalència d'àrees. Demostració clàssica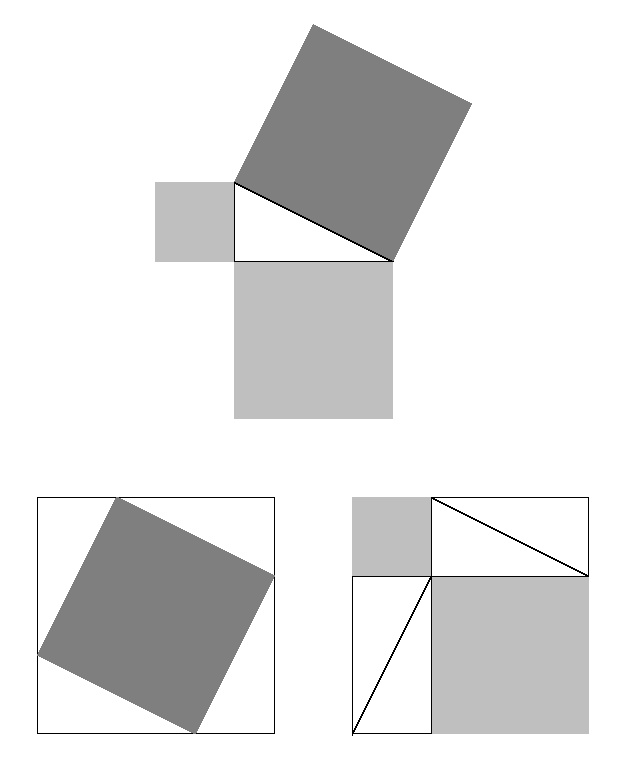
Demostració de Plató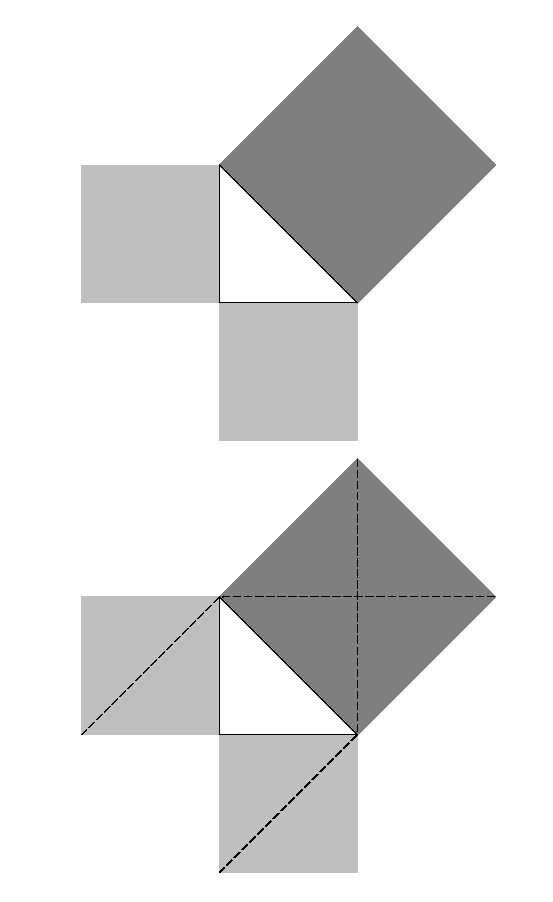
Demostració d'Ibn Qurra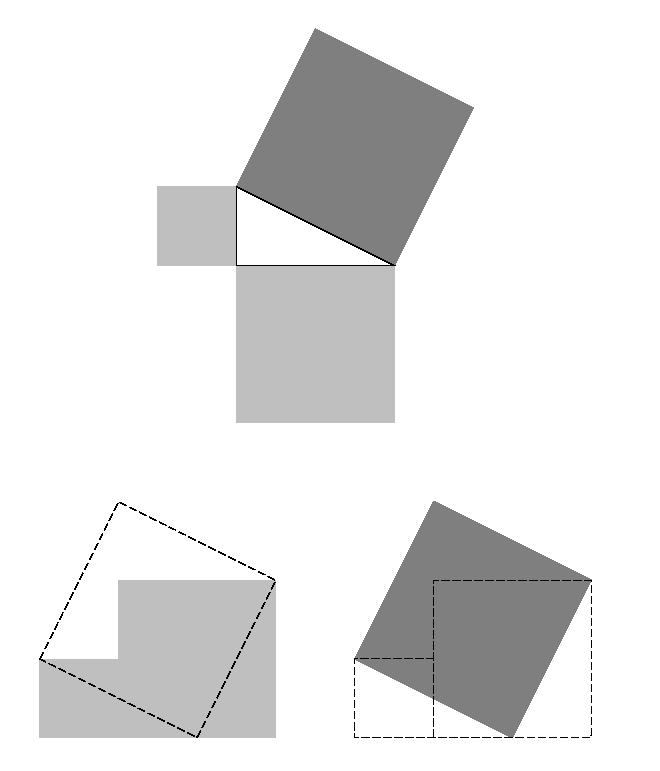
Demostració de Perigal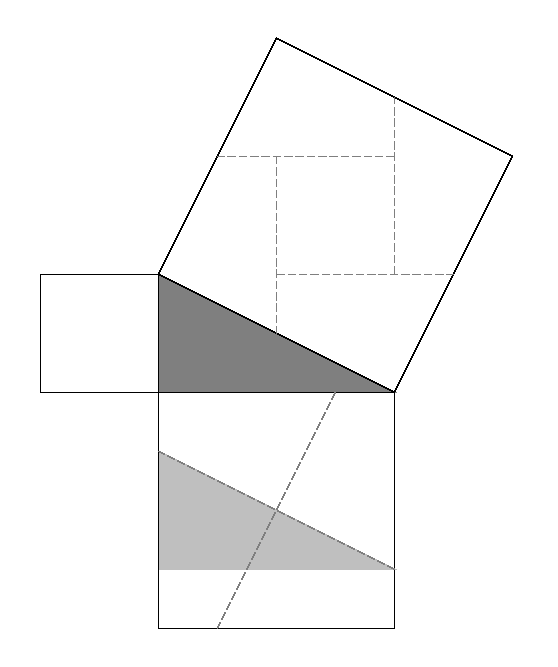
Demostració d'Anaricio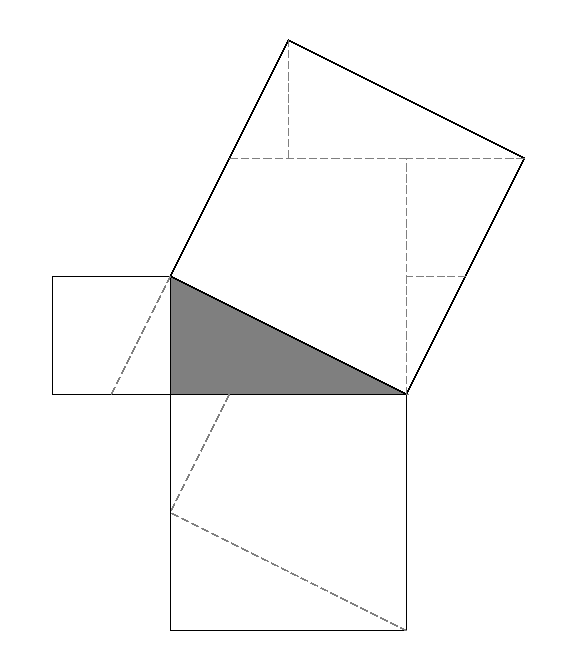
|
|
Tornar a la pàgina principal. |