Productes amb vectors

 

La perpendicularitat i el producte escalar

A 2D és fàcil comprovar que dos vectors del tipus (a,b) i (−kb,ka) són perpendiculars

1. Un exemple de dos vectors perpendiculars.

Per tant, és evident establir que dos vectors A=(a1,a2) i B=(b1,b2) seran perpendiculars si i només si verifiquen a1b1+ a2b2=0. Escriurem aquesta relació com A·B.

I si no són perpendiculars, què significa el resultat a1b1+a2b2?

Si a1=b1 i a2=b2, és a dir, si són dos vectors idèntics, el resultat és el quadrat del mòdul del vector: A·A=|A|2. Però, i si no són idèntics?

Amb tres vectors A, B i A−B podem formar un triangle. En aquest triangle es verifica el teorema del cosinus:

|A−B|2 = |A|2 + |B|2 − 2 |A||B| cos α

Substituim el primer membre aplicant l'equivalència anterior

(A−B)·(A−B) = |A|2 + |B|2 − 2 |A||B| cos α

Desenvolupant el primer membre

A·A −B·A −A·B +B·B = |A|2 + |B|2 − 2 |A||B| cos α

Simplifiquem

−B·A −A·B = − 2 |A||B| cos α

Per construcció, la relació és commutativa, per tant

−2 A·B = − 2 |A||B| cos α

Finalment, simplificant factors, queda

A·B = |A||B| cos α

Definim el producte escalar de dos vectors del pla A i B com A·B=a1b1+a2b2, i verifica A·B = |A||B| cos α, que s'interpreta com |A| vegades la projecció de B sobre A (o a la inversa, |B| vegades la projecció d' A sobre B).

Si extenem aquesta definició a vectors de l'espai, A·B=a1b1+a2b2+a3b3, és immediat veure que el raonament amb el teorema del cosinus és aplicable i obtenim la mateixa conclusió.

 

L'obtenció d'un vector perpendicular: el producte vectorial

Volem aconseguir un vector C a partir de dos vectors coneguts A i B.

Aplicant la propietat del producte escalar sobre els vectors perpendiculars podem dir que el vector buscat ha de verificar C·A=0 i C·B=0. Desenvolupant aquestes condicions arribem a un sistema de dues equacions

a1c1 + a2c2 + a3c3 = 0
b1c1 + b2c2 + b3c3 = 0

Aquest sistema és compatible indeterminat (hi ha infinits vectors que són solució, tot i que tots ells són proporcionals entre si), i si els vectors A i B no són proporcionals el sistema té un grau de llibertat, per això les solucions depenen d'un paràmetre:

Sembla lògic prendre com a valor de c3 el denominador de les anteriors expressions. Amb aquest valor, a més de simplificar les expressions, aconseguim que l'orientació del vector resultant sigui positiva i que, quan els vectors A i B són perpendiculars, el seu mòdul sigui el producte dels mòduls d' A i B.

 
| −a3 a2 |
| −b3 b2 |
 
c1 =
c3
 
| a1 a2 |
| b1 b2 |
 
i
 
| a1 −a3 |
| b1 −b3 |
 
c2 =
c3
 
| a1 a2 |
| b1 b2 |
 

Si C=( a2b3 − a3b2 , a3b1 − a1b3 , a1b2 − a2b1 ), el quadrat del seu mòdul serà

(a2b3 − a3b2)2 + (a3b1 − a1b3)2 + (a1b2 − a2b1)2

Desenvolupant els quadrats

a22b32 + a32b22 −2 a2b3 a3b2 + a32b12 + a12b32 −2 a3b1 a1b3 + a12b22 + a22b12 −2 a1b2 a2b1

Factoritzant els termes dobles

a22b32 + a32b22 + a32b12 + a12b32 + a12b22 + a22b12 − a1b1 ( a2b2 a3b3 ) − a2b2 ( a1b1 a3b3 ) − a3b3 ( a1b1 a2b2 )

i aplicant la condició de perpendicularitat d' A i B, a1b1 + a2b2 + a3b3 = 0, queda

a22b32 + a32b22 + a32b12 + a12b32 + a12b22 + a22b12 + a1b1 a1b1 + a2b2 a2b2 + a3b3 a3b3

Si tornem a factoritzar

a12 ( b12 + b22 + b32 ) + a12 ( b12 + b22 + b32 ) + a12 ( b12 + b22 + b32 )

Per tant, finalment obtenim

( a12 + a22 + a32 ) ( b12 + b22 + b32 )

Definim aquest nou vector com el producte vectorial d'A i B:

A × B = ( a2b3 − a3b2 , a3b1 − a1b3 , a1b2 − a2b1 )

que es recorda fàcilment expressat com a determinant:

  | i j k |
A × B = | a1 a2 a3 |
  | b1 b2 b3 |

Quan els vectors A i B no són perpendiculars, es pot demostrar que el seu mòdul és |A||B| sin α, essent α l'angle que formen els vectors A i B.

Ja hem trobat abans que el |A × B|2 és

a22b32 + a32b22 −2 a2b3 a3b2 + a32b12 + a12b32 −2 a3b1 a1b3 + a12b22 + a22b12 −2 a1b2 a2b1

Aquesta expressió coincideix amb la que s'obté de |A|2 |B|2 − (A · B)2

( a12 + a22 + a32 ) ( b12 + b22 + b32 ) − (a1b1+a2b2+a3b3)2

Desenvolupant-ho,

a12b12 + a12b22 + a12b32 + a22b12 + a22b22 + a22b32 + a32b12 + a32b22 + a32b32 − a12b12 − a22b22 − a32b32 −2 a1b1 a2b2 −2 a1b1 a3b3 −2 a2b2 a3b3

Per tant, si |A × B|2 = |A|2 |B|2 − (A · B)2

substituint el producte escalar, |A × B|2 = |A|2 |B|2 − (|A| |B| cos α )2

desenvolupant el quadrat |A × B|2 = |A|2 |B|2 − |A|2 |B|2 cos2 α

traient factor comú |A × B|2 = |A|2 |B|2 (1− cos2 α)

per tant |A × B|2 = |A|2 |B|2 sin2 α

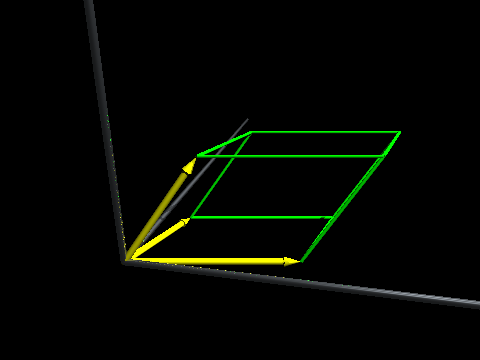
Amb aquesta expressió, la interpretació del producte vectorial de dos vectors és immediata: és un vector perpendicular als dos donats (fig. 2) tal que el seu mòdul és l'àrea del paral·lelogram que generen els dos donats (fig. 3).

2. El producte vectorial dóna un vector perpendicular als dos donats.

3. El mòdul del producte vectorial dóna l'àrea del paral·lelogram generat pels vectors.

La combinació dels dos productes: el producte mixt

De la mateixa manera que dos vectors no proporcionals (o linealment independents) generen un paral·lelogram, tres vectors l.i. generen un paral·lelepípede (fig. 4).

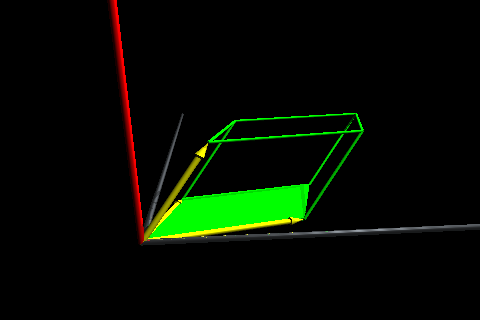
4. El paral·lelepípede generat per 3 vectors.

Considerem els vectors A i B que generen el paral·lelogram (fig. 5). El mòdul del vector A × B és l'àrea d'aquest paral·lelogram.

5. El paral·lelepípede generat per 3 vectors, amb l'àrea de la base i el vector que la representa.

Per tant, el doble producte (A × B) · C donarà la projecció del vector C sobre A × B, és a dir, l'altura del paral·lelepípede multiplicada per l'àrea de la seva base, és a dir |A × B| |C| cos α, on α és l'angle que hi ha entre els vectors C i A × B, o sigui, el volum del paral·lelepípede.

Si desenvolupem (A × B) · C, obtenim

( a2b3 − a3b2 , a3b1 − a1b3 , a1b2 − a2b1 ) · (c1,c2,c3)
a2b3c1 − a3b2c1 + a3b1c2 − a1b3c2 + a1b2c3 − a2b1c3

expressió que coincideix amb el desenvolupament del determinant d'ordre 3 dels vectors A, B i C.

Per tant, podem dir que (A × B) · C = det ( A, B, C ), que el valor del determinant de tres vectors és el volum del paral·lelepípede que generen.

 

 

 

 

Les imatges s'han creat amb el programa POVRAY.

 

 

Copyright © Jaume Serra Nogués, 2010.
Teniu permís per a copiar, distribuir i/o modificar aquest document en les condicions de la Llicència de Documentació Lliure del GNU, versió 1.1 o qualsevol versió posterior publicada per la Fundació per al Programari Lliure (Free Software Foundation), http://www.gnu.org/copyleft/fdl.html.