Algunes activitats d'estadística i probabilitat amb la Wiris

>>

Continguts (conceptes i procediments)

Gràfics

Aquesta secció consta dels apartats següents:

• Introducció.
• Tipus de gràfics:
  • Diagrama de barres (horitzontal o vertical).
  • Pictograma.
  • Diagrama de sectors.
  • Perfil: ortogonal o radial.
  • Histograma i polígon de freqüències. Corba de freqüències.
  • Cartograma.
  • Piràmide de població.
  • Gràfics evolutius (sèries temporals) i comparatius.
• Activitats.

Introducció

La idea de presentar les dades en forma de gràfic és veure, d'una ràpida ullada, quin és el comportament global de la distribució de les dades (cap a on cauen les dades, si estan juntes o separades, etc).

Tipus de gràfics

• Diagrama de barres (vertical o horitzontal).

  En uns eixos cartesians es representa algun tipus de freqüència en funció del valor de la variable estadística. S'utilitzen per a variables qualitatives i quantitatives discretes amb pocs valors diferents de la variable, on no cal fer una agrupació de les dades en intervals.

  Vegem en primer lloc un exemple per a variable qualitativa:

  Partit	ni (vots)
  DPT	1700
  LA	2000
  TC	1300

  

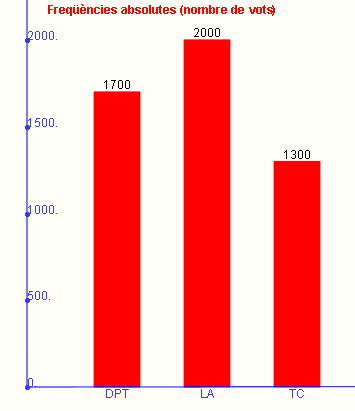
Ara vegem uns exemples per a la següent variable quantitativa discreta:

xi (nombre de cotxes/família)	ni (nombre de famílies)	fi	Fi
0	3	0,3	0,3
1	4	0,4	0,7
3	2	0,2	0,9
4	1	0,1	1
Totals-->	N==	=1

Els tres gràfics que acabem de presentar han estat fets amb la Wiris (vegeu l'activitat act0005.html d'aquesta pàgina).

• Pictograma.

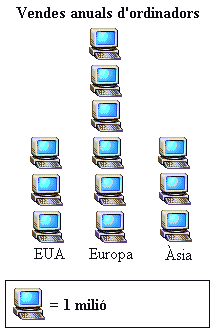
  Són gràfics de poca fiabilitat en què es representen generalment les freqüències de variables qualitatives o quantitatives discretes amb figures que són en altura o en àrea proporcionals a aquestes freqüències. De vegades estan fets de la repetició d'un patró unitat.

  

  

• Diagrama de sectors.

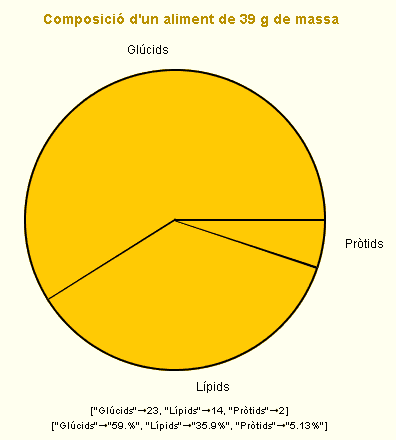
  S'utilitzen per representar variables qualitatives. Cada sector del gràfic té una amplitud angular proporcional a la seva freqüència. Vegem un exemple: suposem que el contingut (en grams) de 39 g d'un aliment és el següent:

  Component	massa (g)
  Glúcids	23
  Lípids	14
  Pròtids	2

  Si interpretem com a freqüències (absolutes) la massa de cada tipus de component, el diagrama de sectors corresponents (fet amb la Wiris a l'activitat act0006.html, per cert), és el següent:

  

  

• Perfil: ortogonal o radial.

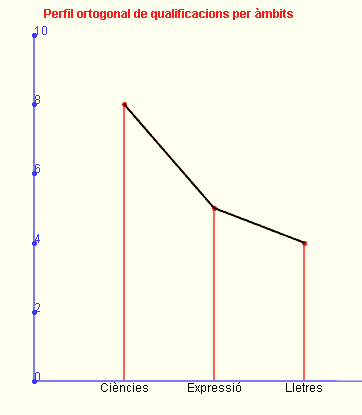
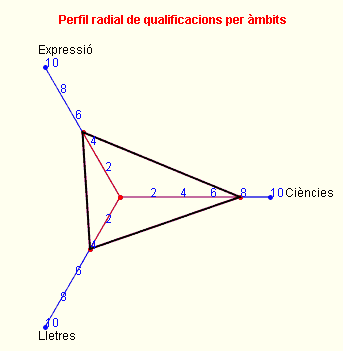
Són gràfics que s'utilitzen sobre tot en psicologia i en ciències de l'educació per captar d'una ullada diverses característiques d'un determinat individu. Si considerem les notes d'un alumne en tres àmbits: àmbit de ciències, un 8; àmbit de lletres, un 4; àmbit d'expressió, un 5, s'interpreta que les notes fan el paper de freqüències.

Els perfils ortogonal i radial corresponents a aquest exemple es presenten a continuació (s'han realitzat amb la Wiris) i estan treballats a l'activitat act0007.html d'aquesta pàgina.







• Histograma i polígon de freqüències. Corba de freqüències.

  S'utilitza per a variable quantitativa contínua (o discreta que pren molts valors diferents i ha estat agrupada en intervals). Els valors de la variable apareixen en abscisses i, en ordenades, apareixen les freqüències. Així de simple és quan els intervals són de la mateixa amplitud. Si no ho són, els histogrames de freqüències no acumulades s'han de fer no de les freqüències sinó de les densitats de freqüències (freqüències/amplitud d'interval).

  Vegem un exemple: medim "l'altura" (en cm) de diversos nadons en néixer i els resultats, agrupats en intervals de la mateixa amplitud, són els següents:

  Interval	Marca de classe xi	ni	Ni
  [40, 43)	41,5	25	25
  [43, 46)	44,5	0	25
  [46, 49)	47,5	105	130
  [49, 52)	50,5	137	267
  [52, 55)	53,5	108	375
  [55, 58)	56,5	62	437
  Totals-->		N==437

  Amb la Wiris hem fet els següents gràfics: (vegeu activitat act0008.html)

  

  

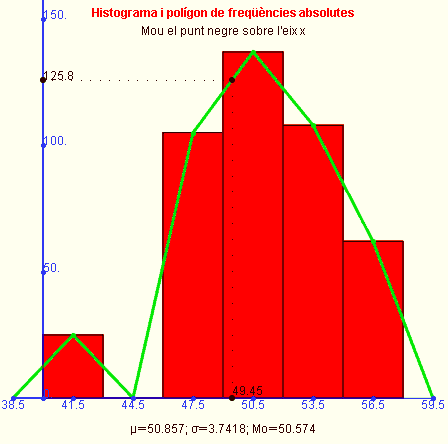
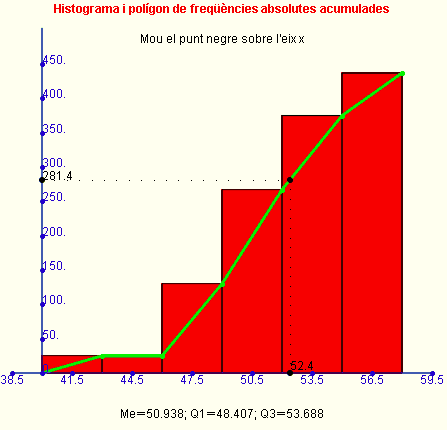
  Per cert, en els dos histogrames anteriors apareixia una línia poligonal que anomenàvem polígon de freqüències. Quan la línia, en lloc de ser una línia poligonal, és una línia suau, traçada "a mà", ja no s'anomena políton de freqüències sinó que s'anomena corba de freqüències. En les activitats fetes amb la Wiris, si es mou el punt negre sobre l'eix x es pot veure com va variant la freqüència corresponent.

  

• Cartograma.

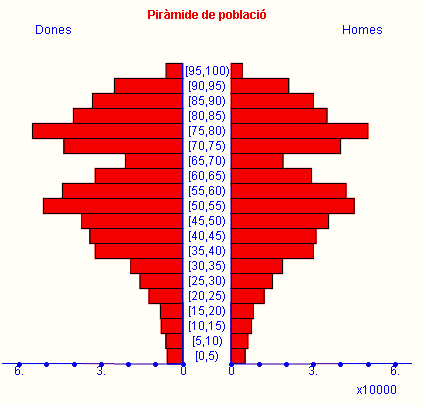
  És un mapa on les diverses regions s'acoloreixen segons el valor de la variable estadística.

  

  

• Piràmide de població.

  Està feta oposant dos histogrames (un per a cada sexe -dones i homes-), els quals tenen, en les seves abscisses, les edats de la població i en ells es representen freqüències absolutes (nombre de persones de cada edat).

  Vegeu una taula i el corresponent histograma fet amb la Wiris (act0009.html).

  	[0,5)	[5,10)	[10,15)	[15,20)	[20,25)	[25,30)	[30,35)	[35,40)	[40,45)	[45,50)	[50,55)	[55,60)	[60,65)	[65,70)	[70,75)	[75,80)	[80,85)	[85,90)	[90,95)	[95,100)
  D	5500	6100	7800	8100	12300	15600	19000	32000	34000	37000	51000	44000	32000	20900	43550	55000	40000	33000	25000	6000
  H	5000	6000	7340	8000	12000	15020	18750	30000	31000	35592	45000	42000	29340	18900	40020	50020	35000	30000	21000	4000

   

  

  

• Gràfics evolutius (sèries temporals) i comparatius.

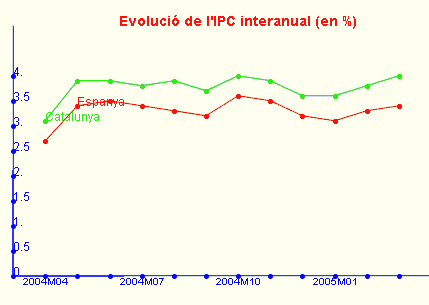
  Representen el valor d'una variable estadística en funció del temps. Quan en un gràfic es combinen dues o més variables es diu que són comparatius. Vegem un exemple: es disposa dels IPC interanuals de Catalunya i Espanya entre abril de 2004 i març de 2005. Les dades es presenten a la taula següent:

  	2004M04	2004M05	2004M06	2004M07	2004M08	2004M09	2004M10	2004M11	2004M12	2005M01	2005M02	2005M03
  Catalunya	3,1	3,9	3,9	3,8	3,9	3,7	4	3,9	3,6	3,6	3,8	4
  Espanya	2,7	3,4	3,5	3,4	3,3	3,2	3,6	3,5	3,2	3,1	3,3	3,4

  El gràfic corresponent, fet amb la Wiris (activitat act0010.html del final d'aquesta pàgina), és el següent:

  

  

Activitats

• Act0005.html. Diagrama de barres per a variable qualitativa. Diagrames de barres per a variable quantitativa discreta (freqüències acumulades i sense acumular).
• Act0006.html. Diagrama de sectors.
• Act0007.html. Perfils: ortogonal i radial.
• Act0008.html. Histogrames i polígons de freqüències.
• Act0009.html. Piràmides de població.
• Act0010.html. Gràfics evolutius (sèries temporals) i comparatius.