Algunes activitats d'estadística i probabilitat amb la Wiris

>>

Continguts (conceptes i procediments)

Altres paràmetres: moments

Aquesta secció consta dels apartats següents:

• Moment d'ordre r respecte de c.
• Moments centrals.
• Moments respecte de l'origen.
• Algunes qüestions relatives a moments. Relacions. Forma de la distribució de dades.

Moment d'ordre r respecte de c.

Els moments d'una distribució de dades són uns números que la caracteritzen, de manera que cada distribució de dades té una sèrie de moments i dues distribucions de dades són iguals si i només si tenen tots els seus moments iguals.

S'anomena moment d'ordre r respecte de c a l'expressió següent:

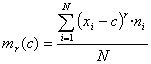o equivalentment

Els moments més coneguts són els moments respecte de la mitjana (anomenats moments centrals, és a dir, amb c=) i els moments respecte a 0 (anomenats moments respecte a l'origen, és a dir, amb c=0).

Moments centrals.

Com hem dit abans són un cas partircular de moments en el qual c=. Se simbolitzen per m_r. Llavors, la seva expressió és:

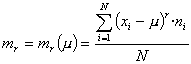o equivalentment

És fàcil veure que els primers moments centrals valen:

m₀=1

m₁=0

m₂=.

La Wiris disposa de la funció moment_centrat(r,X), que permet calcular els moments d'ordre r de la llista de dades X (consulteu la part de l'ajuda relativa a l'índex de funcions per verue els detalls d'ús).

Moments respecte de l'origen.

Com hem dit més amunt són un cas partircular de moments en el qual c=0. Se simbolitzen per a_r. Llavors, la seva expressió és:

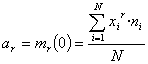o equivalentment

És fàcil veure que els primers moments respecte de l'origen valen:

a₀=1

a₁=

a₂=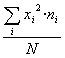, és a dir, la mitjana dels quadrats de x_i.

Algunes qüestions relatives a moments. Relacions. Forma de la distribució de dades.

Si recordem la fórmula següent, vista més amunt,

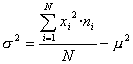
es pot reescriure, utilitzant moments, així:

m₂=a₂-a₁²

D'altra banda, és poden definir quantitats (utilitzant moments) que ens informen sobre el biaix o la punxagudessa de la distribució, és a dir, sobre la seva forma:

• Coeficient de biaix (o d'asimetria) de Fisher (A_F):

  Hi ha diversos coeficients de biaix (coeficients d'asimetria) però, per simplificar, només tractarem del coeficient de biaix de Fisher. Es defineix així:

  A_F=m₃/³

  i resulta que

  • si A_F>0 llavors la distribució està esbiaixada cap a la dreta (es diu que té biaix positiu).
  • si A_F<0 llavors la distribució està esbiaixada cap a l'esequerra (es diu que té biaix negatiu).
  • si A_F=0 llavors la distribució és simètrica (no està esbiaixada, és a dir, una recta vertical que passés per la mitjana de la distribució faria com "de mirall" de la part esquerra i la part dreta de la distribució).

  Vegem uns exemples de distribució esbiaixada cap a la dreta, no esbiaixada i simètrica (respectivament):

  

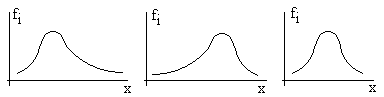
  Cal dir que el coeficient d'asimetria amb què treballa la Wiris no és el que hem tractat aquí (consulteu a l'ajuda de la Wiris l'índex alfabètic per veure la definició del que ella utilitza, que s'anomena coeficient_de_assimetria).

• Coeficient de punxesa (o curtosi):

  Ens informa de si la distribució de dades és més punxaguda o menys punxaguda que la distribució normal que té la mateixa mitjana i desviació típica . La distribució normal s'estudiarà més endavant.

  Es diu que la distribució normal és, quant a punxesa, mesocúrtica. Aquelles distribucions que són més punxagudes que la normal de la mateixa i la mateixa es diu que són leptocúrtiques i les que en són menys, platicúrtiques.

  Si definim com a coeficient del moment de punxesa així: A₄=m₄/⁴, resulta que la normal té A₄=3.

  Si definim com a coeficient de punxesa així: g₄=A₄-3, resulta que la normal té g₄=0. Per tant, quan una distribució té

  • g₄>0, és leptocúrtica (és més punxaguda que la normal que té la mateixa i la mateixa );
  • g₄<0, és platicúrtica (és menys punxaguda que la normal que té la mateixa i la mateixa );
  • g₄=0, és mesocúrtica (és igual de punxaguda que la normal que té la mateixa i la mateixa ).

  Vegem una il·lustració que visualitza les possibles situacions:

  

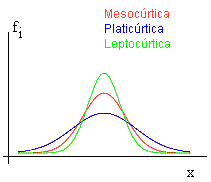
  La funció coeficient_de_punxesa(X) amb què treballa la Wiris permet calcular per a la llista X el que nosaltres hem anomenat coeficient de punxesa (consulteu, a l'ajuda, l'índex alfabètic per veure'n els detalls).

  Amb la Wiris hem dissenyat una activitat (act0014.html) amb la qual es genera una distribució de dades (se suposa que les dades s'han agrupat en intervals), es construeix l´histograma i el polígon de freqüències corresponent, es veu quina és la forma de la distribució normal que té la mateixa mitjana i la mateixa desviació típica i es calculen alguns paràmetres que ens informaran de la forma de la distribució de dades (asimetria i punxesa). A continuació mostrem una finestra gràfica feta amb aquesta activitat de la Wiris:

  

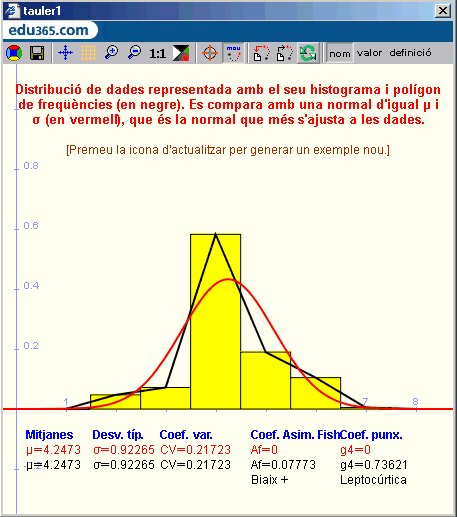
Activitats:

• Act0014.html. Alguns paràmetres d'una distribució de variable contínua. Distribució normal de la mateixa mitjana i desviació típica. Histograma i polígon de freqüències. Forma: asimetria i punxesa.