>>
|
|
Algunes activitats d'estadística i probabilitat amb la Wiris |
>>
|
|
Continguts (conceptes i procediments) |
A més de les activitats del final de la pàgina, aquesta secció consta dels apartats següents:
Paràmetres de dispersió més coneguts:
Són valors que ens indiquen si les dades de la distribució estan concentrades o disperses. Per cert, per al seu càlcul, quan la variable s'hagi agrupat en intervals, determinarem les marques de classe i treballarem tranquil·lament amb elles tal com ja hem fet quan determinàvem els paràmetres de posició.
És el més fàcil de calcular, ja que és la diferència entre els valors màxim i mínim de la variable:
rang = xmàx - xmín
És la mitjana aritmètica ponderada del valor absolut de les desviacions respecte a la mitjana, és a dir,
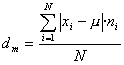
Si tenim la informació en forma de taula, podem escriure-ho així:
):
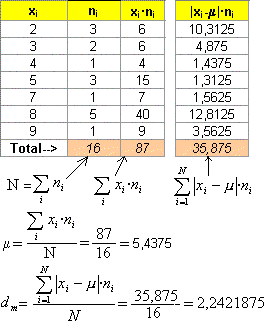
És la mitjana aritmètica ponderada dels quadrats de les desviacions respecte a la mitjana, és a dir,
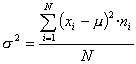o també 
Aquestes expressions també es poden reescriure així:
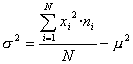o també 
Si el càlcul es vol fer a mà, posant les dades en forma de taula, podem escriure el següent i utilitzar les fórmules de la línia immediatament anterior o les de dues línies més amunt.
):
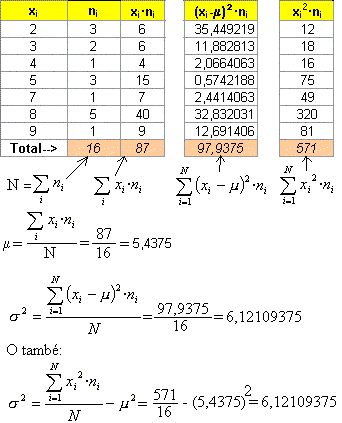
És l'arrel quadrada de la variança (per tant, una vegada calculada aquesta, trobar la desviació típica és una cosa ben senzilla!):
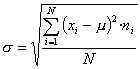o també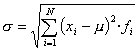 
que es poden reescriure així:
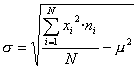o també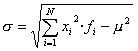 
En l'exemple de la taula anterior, després de fer l'arrel ens sortiria
=2,474084427.
És el quocient entre la desviació típica i la mitjana i es pot donar en tant per un o en tant per cent:
En l'exemple anterior ens sortiria CV=2,474084427/5,4375=0,455004=45,4004%.
Altres paràmetres de dispersió.
És la diferència entre el 3r i el 1r quartil:
rang interquartílic = Q3 - Q1
És la meitat del rang interquartílic:
rang semiinterquartílic = (Q3 - Q1)/2
Activitats