Algunes activitats d'estadística i probabilitat amb la Wiris

>>

Continguts (conceptes i procediments)

Paràmetres de posició

A més de les activitats del final de la pàgina, aquesta secció consta dels apartats següents:

• Definició de paràmetres de posició.
• Paràmetres de posició centrals més coneguts.
  • Moda.
  • Mitjana aritmètica.
  • Mediana.
• Altres paràmetres de posició.
• Activitats.

Definició de paràmetres de posició centrals.

Són valors al voltant dels quals "s'agrupen" les dades.

Paràmetres de posició centrals més coneguts.

• Moda (Mo):

  És el valor que té una freqüència absoluta (o relativa) més alta. Pot ser únic (distribucions unimodals) o no (distribucions multimodals: bimodals si tenen 2 modes, trimodals si en tenen 3, etc.).

  Determinació de la moda:

  • Per a variable estadística qualitativa (o quantitativa discreta amb pocs valors diferents de la variable): és fàcil, ja que només cal mirar quin és el valor que té una freqüència absoluta (o relativa) més alta (és a dir, apliquem la definició de moda per calcular-la).
  • Per a variable estadística que ha estat sotmesa a una agrupació de les dades (variable quantitativa contínua o discreta amb molts valors diferents de la variable): s'anomena interval de classe modal aquell que té una freqüència absoluta (o relativa) major. De manera aproximada podem dir que la moda és la marca de classe de l'interval de classe modal (és a dir, és el centre de l'interval de classe modal). També es pot dir que la moda és la marca de classe de l'interval de classe modal en el cas que els intervals anterior i posterior al modal tinguin la mateixa freqüència, com en el dibuix següent:

   

  

Finalment, si els intervals anterior i posterior al modal tenen freqüències diferents, es pot fer una determinació gràfica de la moda tal com s'indica en el gràfic següent:



Llavors, la fórmula matemàtica que ens permetria calcular la moda seria aquesta:



on:

L_i = extrem inferior de l'interval de classe modal

n_i = és la freqüència absoluta de la classe modal

n_i-1 = és la freqüència absoluta de l'interval anterior a la classe modal

n_i+1 = és la freqüència absoluta de l'interval posterior a la classe modal

h = amplitud de l'interval



• Mitjana aritmètica ():

  Es calcula mitjançant alguna de les dues fórmules equivalents següents:

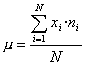  o bé, tenint en compte que n_i/N=f_i, .

  Si el càlcul es fa a mà, amb una taula, podem organitzar la informació així:

  

  Quan s'han agrupat les dades en intervals, si se suposa que les dades estan distribuïdes uniformement en cada interval, la mitjana aritmètica es calcula amb les fórmules anteriors tenint en compte que els x_i són les marques de classe de cada interval i n_i. les freqüències absolutes de cada interval.

  Quan se sobreentén que es parla de la mitjana aritmètica se li pot dir simplement mitjana, però si pot haver confusió, s'ha de dir mitjana aritmètica, ja que hi ha altres mitjanes (harmònica, geomètrica...).

  

• Mediana (Me):

  És el valor que deixa per sota d'ell el 50% de les dades, és a dir, si s'ordenen les dades, és aquell valor que ocupa la posició central. Només té sentit per a variables quantitativas.

  El seu càlcul per a variables quantitatives discretes (no agrupades en intervals) és fàcil: si hi ha un total de N dades i ordenem les dades de manera creixent, llavors:

  • Si N és parell, la Me és la mitjana aritmètica dels valors que ocupen les posicions N/2 i (N/2)+1.
  • Si N és imparell, la Me és el valor que ocupa la posició (N+1)/2.

  Quan les dades han estat agrupades en intervals cal esbrinar l'interval que és la classe mediana. Per determinar-lo començo a mirar la freqüència absoluta acumulada (o la relativa acumluada) dels intervals des dels que tenen una marca de classe més petita a aquells que la tenen més gran. El primer interval que compleixi tenir una freqüència absoluta acumulada superior a N/2 (o, equivalentment, tenir una freqüència relativa acumulada superior a 0,5) és la classe mediana.

  Una vegada coneguda la classe mediana, si anomenem:

  L_i = extrem inferior de l'interval de classe mediana

  N = nombre de dades

  N_i-1 = és la freqüència absoluta acumulada de l'interval anterior a la classe mediana

  n_i = és la freqüència absoluta de la classe mediana

  h = amplitud de l'interval

  Resulta que la mediana Me ve donada per la fórmula següent:

  

  

  

Altres paràmetres de posició.

• Quartils.

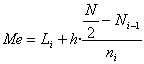
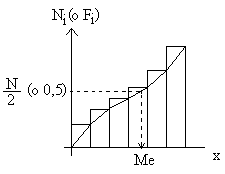
  S'anomenen quartils als valors de la variable que parteixen la distribució en 4 parts iguals (entre cada quartil hi ha un 25% de les dades). Per determinar els quartils ordenem els valors de la variable de manera creixent.

  • El primer quartil (Q₁) deixa per sota d'ell el 25% de les dades.

  Es determina d'una manera semblant a la mediana:

  Si les dades no estan agrupades, quan N és divisible entre 4, el primer quartil és la mitjana entre els valors de la variable que ocupen les posicions N/4 i (N/4)+1. En cas que N no sigui divisible entre 4, el primer quartil és el primer valor de la variable que és superior a N/4.

  Si les dades estan agrupades en intervals, primer busquem l'interval que conté el primer quartil (haurà de ser el interval que, tenint una marca de classe el més petita possible, té una freqüència absoluta acumulada superior a N/4 -o equivalentment, una freqüència relativa acumulada superior a 0,25). Després caldrà aplicar la fórmula següent:

  

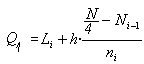
  on, com és d'esperar:

  L_i = extrem inferior de l'interval (que conté el quartil)

  N = nombre de dades

  N_i-1 = és la freqüència absoluta acumulada de l'interval anterior a l'interval que conté el quartil

  n_i = és la freqüència absoluta de l'interval que conté el quartil

  h = amplitud de l'interval

  • El segon quartil (Q₂) deixa per sota d'ell el 50% de les dades (és la mediana i ja el sabem calcular!).
  • El tercer quartil (Q₃) deixa per sota d'ell el 75% de les dades. Si les dades no estan agrupades, quan N és divisible entre 4, el tercer quartil és la mitjana entre els valors de la variable que ocupen les posicions 3N/4 i (3N/4)+1. En cas que N no sigui divisible entre 4, el tercer quartil és el primer valor de la variable que és superior a 3N/4.

    Si les dades estan agrupades en intervals, primer busquem l'interval que conté el tercer quartil (haurà de ser el interval que, tenint una marca de classe el més petita possible, té una freqüència absoluta acumulada superior a 3N/4 -o equivalentment, una freqüència relativa acumulada superior a 0,75). Després caldrà aplicar la fórmula següent:

    

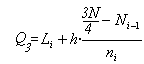
    (i el significat de cada lletra ara ja és conegut -consulteu la llegenda per al primer quartil-).

• Percentils.

  De manera semblant als quartils, però generalment per a variable que ha estat agrupada en intervals (només donarem la definició en aquest cas), es poden definir els percentils (o centils) P_k. El percentil P_k és el valor de la variable tal que per sota d'ell hi ha un k% de les dades.

  Per calcular-los, primer busquem l'interval que conté el primer quartil (haurà de ser el interval que, tenint una marca de classe el més petita possible, té una freqüència absoluta acumulada superior a k·N/100 -o equivalentment, una freqüència relativa acumulada superior a k/100-). Després caldrà aplicar la fórmula següent:

  

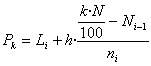
  on el significat de les lletres ja es conegut.

  Observeu que la fórmula del percentil ens permet calcular quin percentatge de dades (quina k) hi ha per sota d'un cert valor x=P_k de la distribució. Vegem un exemple: si em diuen que calculi quin % de les dades són menors o iguals que x=25 en una certa distribució de dades el que hauríem de fer és identificar P_k amb 25, és a dir, substituir P_k=25 en la fórmula del percentil i, esbrinant prèviament el valor de totes les lletres que apareixen a la fórmula, trobar la k, que és el percentatge que busco.

  Si l'exercici em diu que trobi quin percentatge de dades hi ha entre x₁=25 i x₂=67, el que hauria de fer és, utilitzant el procediment trobat en l'apartat anterior, trobar les k₁ i k₂ corresponents a aquestes x i restar els percentatges obtinguts, és a dir, fer k₂-k₁.

  Els percentils P₁₀, P₂₀, P₃₀, P₄₀, P₅₀, P₆₀, P₇₀, P₈₀ i P₉₀ s'anomenen decils i se'ls simbolitza per D₁, D₂, D₃, D₄, D₅, D₆, D₇, D₈ i D₉.

Activitats

• Act0012.html. Determinació de mitjana, moda, mediana i quartils per a variable discreta no agrupada en intervals.
• Act0008.html. Histogrames i polígons de freqüències per a variable agrupada en intervals. Determinació de mitjana, desviació típica, moda, mediana i quartils.