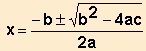En aquesta activitat veuràs com calcular el vèrtex de la funció quadràtica de la forma y = ax² + bx + c i com trobar els punts d'intersecció d'una paràbola amb els eixos de coordenades. Veuràs també la relació entre aquest darrer càlcul i l'equació de segon grau.

Hem vist que el vèrtex d'una paràbola de la forma y = a(x - p)² + q és el punt (p,q). La forma general de les funcions de segon grau és y = ax² + bx + c, el pas d'una forma a l'altre resulta, en alguns casos, una mica llarg. Una forma alternativa de calcular el vèrtex està basada en les següents propietats:

• La paràbola y = ax² + bx + c té la mateixa forma que y = ax² + bx però desplaçada c unitats verticalment, per tant l'abcissa del vèrtex serà la mateixa per les dues paràboles.
• L'abcissa del vèrtex de y = ax² + bx és la mitjana de les abcisses dels punts de tall de la paràbola amb l'eix d'abcisses, que són x = 0 i x = - b/a
• L'abcissa x_v del vèrtex de y = ax² + bx resulta:

Per exemple, l'abcissa del vèrtex de la paràbola g(x) = 2x² - 4x + 3 és la mateixa que la de f(x) = 2x² - 4x

Els punts de tall de f(x) = 2x² - 4x amb l'eix d'abcisses són (0,0) i (2,0), el punt mitjà d'aquest dos punts és (1,0). Per tant l'abcissa del vèrtex de les dues paràboles és 1 i l'eix de simetria és la recta x = 1.

L'ordenada del vèrtex es calcula substituint el valor 1 a la paràbola corresponent:

f(1) = 2·1² - 4·1 = -2 per tant el vèrtex de f(x) és (1, -2)

g(1) = 2·1² - 4·1 + 3 = 1 per tant el vèrtex de g(x) és (1, 1)

Per comprovar aquesta propietat, activa la següent finestra , mou els punts indicats i utilitza per desplaçar-te si queden els vèrtexs fora de la finestra gràfica:

Per tant per calcular l'abcissa del vèrtex d'una paràbola donada en la forma
y = ax² + bx + c, pots fer servir la fórmula:

Per calcular el punt de tall amb l'eix d'ordenades només cal substituir la x per 0 a l'equació de la paràbola y = ax² + bx + c. Resulta el punt (c,0)

Segons la forma de la paràbola i la situació del vèrtex, tallarà en un punt o dos, o no tallarà a l'eix d'abcisses. Aquestes tres situacions depenen dels valors dels paràmetres a, b i c, i els punts de tall amb l'eix d'abcisses es calculen a partir de l'equació de segon grau ax² + bx + c = 0.

Observa tres situacions diferents amb els exemples següents:

Resol les equacions de segon grau que corresponen a les paràboles de l'exemple anterior, i comprova que els resultats obtinguts coincideixen amb els observats gràficament. Utilitza la fórmula de resolució de l'equació de segon grau:

Resol les equacions de segon grau amb la calculadora WIRIS.

Observa en aquest quadre la relació entre els coeficients de la funció quadràtica, les solucions de l'equació de segon grau i la intersecció amb l'eix d'abcisses de la seva gràfica.

Per realitzar més càlculs accedeix a la calculadora des de l'escriptori de l'edu365.com o bé directament. Al menú Operacions trobaràs l'opció resol equació que et permetran resoldre tot tipus d'equacions. Cal tenir en compte que el símbol que apareix en l'equació equival a = =

Si t'interessa saber més detalls sobre la calculadora WIRIS consulta les ajudes que porta: la Documentació o la Guia Ràpida.