Demostraciones

En esta página demostramos que la sucesión cociente de Fibonacci tiene como límite el número áureo, y después demostramos que a partir de cualquier sucesión que tenga la fórmula de Fibonacci, podemos construir una sucesión cociente que también tiene como límite el número áureo.

 

Cuatro términos consecutivos cualesquiera de esta sucesión son de la forma a, b, a+b, a+2b, observad que cualquier término se puede representar por la fórmula de recurencia An=An-1+An-2, o sea que cada término es la suma de los dos anteriores, por tanto si dividimos la fórmula entre An-1, nos queda: en esta fórmula se ve que la sucesión cociente está acotada superiormente por 2 e inferiormente por 1, y ahora vamos a demostrar mediante el método de inducción completa que la diferencia entre dos términos cualesquiera de la sucesión cociente es menor que cualquier número dado.

En efecto en el cuadro de cálculo vemos como las dos sucesiones (creciente y decreciente) se van acercando progresivamente, formando una sucesión de intervalos encajados que contienen el número áureo. Supongamos que la diferencia entre dos términos consecutivos es menor que un numero dado h, o sea: , vamos a demostrar que la misma desigualdad se cumple para los términos siguientes:

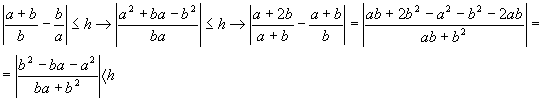
Observad que el valor absoluto del numerador a2+ba-b2 es el mismo que en la última expresión, mientras que el numerador es mayor, por eso podemos afirmar que la última expresión es más pequeña que la primera. Con todo esto hemos demostrado que el límite de las dos sucesiones es el mismo, lo cual quiere decir que:

es decir que el límite de la sucesión cociente cumple la ecuación siguiente: la cual implica que tiene como solución positiva el número áureo.

Ahora vamos a demostrar que en cualquier sucesión que tenga como término general An=An-1+An-2 si formamos la sucesión cociente entre dos términos consecutivos, el límite de ésta también es el número áureo.

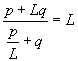En efecto, si la sucesión comienza por dos números p y q cualesquiera, tendría los siguientes términos: p, q, p+q, p+2q, 2p+3q, 3p+5q, .....y por lo tanto el término general de la sucesión cociente de dos términos consecutivos sería: con lo cual si dividimos el numerador y el denominador entre An-1 y calculamos el límite cuando n tiende a infinito nos quedaría: , donde L es el límite de la sucesión cociente de Fibonacci.