
Executa
l'applet
El
professor a l'aula, amb el canó de vídeo, pot utilitzar
aquest applet per reforçar alguns dels conceptes sobre xocs.
De forma orientativa...
En tots els casos és millor començar per les situacions més senzilles (xoc rectilini) per després complicar-ho referint-nos als xocs en el pla.
- Diferència entre xoc elàstic i inelàstic.
- La conservació de la quantitat de moviment es pot observar clarament tant en el xoc elàstic com en l'inelàstic. Segur que el millor serà començar amb els xocs rectilinis i acabar amb els xocs en 2 dimensions.
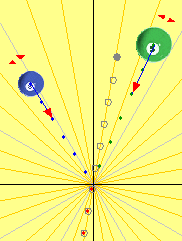
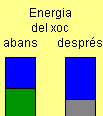
- L'energia perduda en el xoc per efecte Joule, de manera qualitativa, es pot observar clarament en els diagrames de barres de la dreta de l'applet. Lògicament en el xoc elàstic l'energia es conserva i només hi ha transferència d'energia.
- Podem analitzar, qualitativament, en quines condicions d'un xoc inelàstic el percentatge d'energia perduda és mínima o màxima. Per exemple simulant primer un xoc frontal entre dos cotxes i després, amb les mateixes condicions, però un cotxe xocant per darrera contra l'altre.
- Concepte de centre de masses veient que sempre està entre les dues masses però a menys distància de la massa més gran.
- Moviment uniforme del centre de masses en qualsevol xoc (elàstic, inelàstic, en una dimensió, en dues dimensions...).
- Xoc elàstic d'una bola contra la segona bola aturada, especialment si les dues masses són iguals.
- Xoc inelàstic de dues boles d'igual massa quan una d'elles
està quieta. També si una massa és molt més gran que l'altre.
Procediments
També podem utilitzar l'applet per treballar procediments i/o comprovar els resultats obtinguts en la resolució numèrica d'exercicis. Podem calcular per exemple:
- Calcular la velocitat final en un xoc rectilini i inelàstic entre dos objectes.
- Calcular l'energia perduda en un xoc inelàstic.
- Calcular la velocitat, direcció i sentit d'un xoc inelàstic en dues dimensions.
- Trobar la variació de quantitat de moviment de cada bola implicada en un xoc elàstic i comprovar que la variació total és nul·la.
- Comprovar la variació d'energia en un xoc elàstic i analitzar la tranferència entre els dos objectes.
- Comprovar numèricament el resultat final d'un xoc elàstic on un dels dos objectes inicialment està aturat (especialment si les dues masses són iguals).
- Comprovar que en un xoc elàstic la suma de velocitats,
abans i després del xoc, per a cada objecte és la mateixa (v2f + v2i
= v1f + v1i).