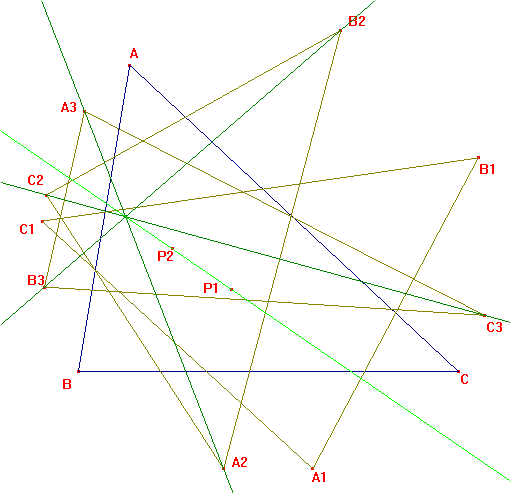
Let P1, P2 be two isogonal points, A1B1C1, A2B2C2 their circumcevian triangles. Let A3B3C3 be the circumcevian triangle of P2 with respect to A1B1C1. The lines A2A3, B2B3, C2C3 concur at a point in the line P1P2. If P1 is the circumcenter; this point is X(24); if P1 is the circumcenter, it is the De Longchamps point.