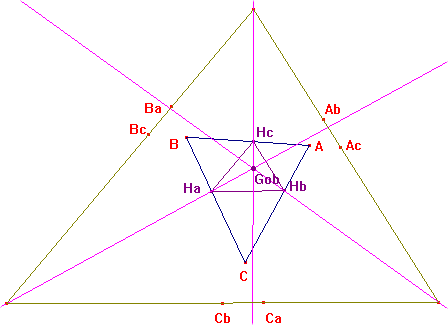
Let HaHbHc be the orthic triangle. Let Ab (resp. Ac) be the homothetic transform of A with center Hb (resp. Hc) and the same ratio. Define analogously Bc, Ba, Ca, Cb (always with the same ratio). The lines AbAc, BcBa, CaCb bound a triangle homothetic to HahbHc with homothetic center the Gob point.