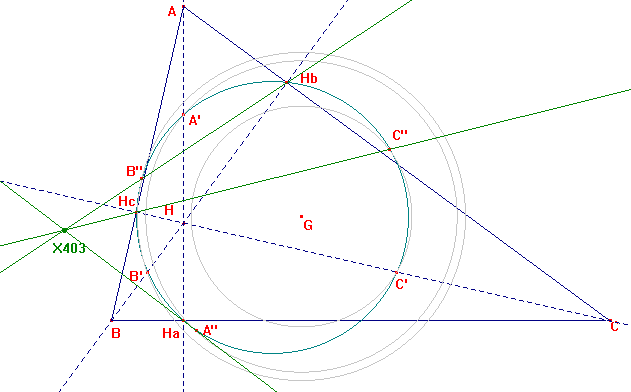
Let H, G be the orthocenter and the centroid of ABC. The altitudes cut the cevian circle of G, H at A’, B’, C’ and the circles centered at G going through A’, B’, C’ cut it again at A”, B”, C”. Let Ha, Hb, Hc be the altitude feet. The lines HaA”, HbB”, HcC” concur at the point X(403).