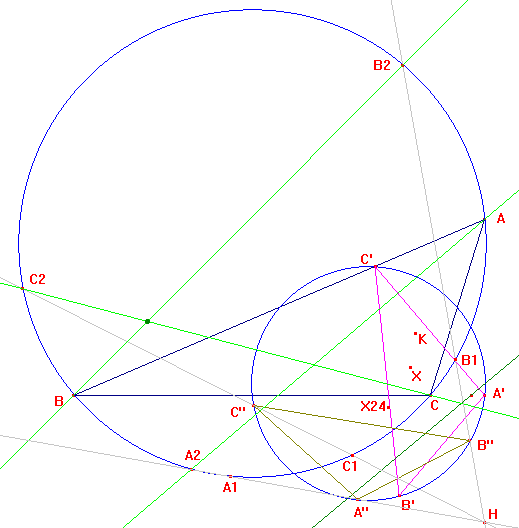
Let P be a point in the tripolar of the cevian product between the symmedian K and the point X(24), A'B'C' its circumcevian triangle, H the orthocenter. The line A'H cuts the circumcircle at A1, A2 (A1 the nearest to H). Define analogously B1, B2, C1, C2. The lines AA2, BB2, CC2 concur.