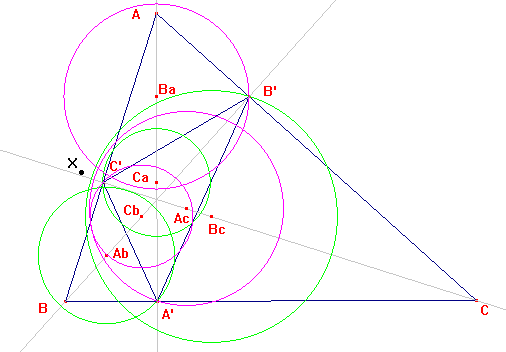
Let A'B'C' the orthic triangle. Let Ab, Ac be the orthogonal projections of A' on BB', CC' and define analogously Bc, Ba, Ca, Cb. The circles (Ab, AbA') - with center Ab and going through A' - (Bc, BcB'), (CaCaC') have radical center X, orthocenter of A'B'C'. The circles (Ac, AcA'), (Ba, BaB'), (Cb, Cbc') have also X as radical center.