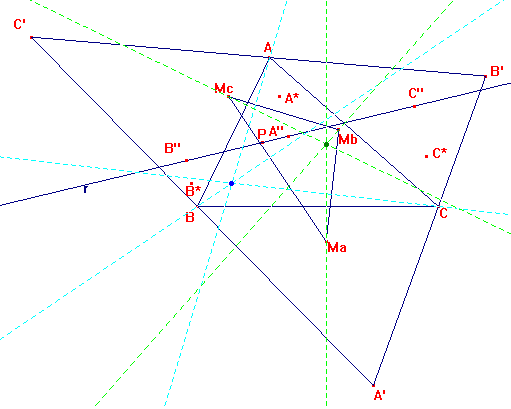
Let P be a point, A'B'C' its antipedal triangle, r a line through P. Let A”, B”, C” be the orthogonal projections of the vertices on r. Let A*, B*, C* be the midpoints of AA”, BB”, CC” and Ma, Mb, Mc the midpoints of A'A*, B'B*, C'C*. The triangles ABC, MaMbMc are orthologic.