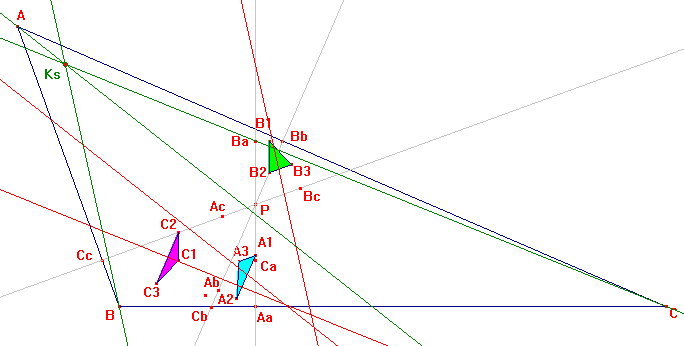
Let P be a point in the Euler line; Aa, Bb, Cc its orthogonal projections on the sides. Let Ab, Ac be the orthogonal projections of Aa on PCc, PCb and define cyclically Bc, Ba, Ca, Cb. Let A1, A2, A3 be the midpoints of PAa, AbAa, AcAa and define cyclically B1, B2, B3, C1, C2, C3. The parallels from A, B, C to the Euler lines of A1A2A3, B1B2B3, C1C2C3 concur at the Kosnita point Ks.