Bisectors
of the sides and circumcentre
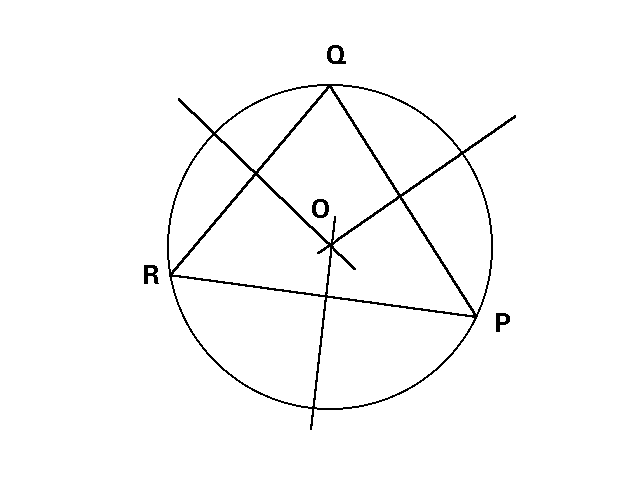 The
three bisectors of the sides of a triangle intersect in a unique point,
the circumcentre, which is the centre of the circumscribed circle. In order
to prove this statement we must only think that each point of the bisector
of the side PQ is equidistant from P and Q. Analogously
each point of the side PR is equidistant from P and R.
The intersection point O of both bisectors is simultaneously equidistant
from P, Q and R. Then
O also belongs to the
bisector of the side QR. Therefore the three bisectors meet in a
unique point. Because O is equally distant from the three vertices,
the circumscribed circle has its centre in O. Let us use this condition
to calculate the equation of the circumcentre:
The
three bisectors of the sides of a triangle intersect in a unique point,
the circumcentre, which is the centre of the circumscribed circle. In order
to prove this statement we must only think that each point of the bisector
of the side PQ is equidistant from P and Q. Analogously
each point of the side PR is equidistant from P and R.
The intersection point O of both bisectors is simultaneously equidistant
from P, Q and R. Then
O also belongs to the
bisector of the side QR. Therefore the three bisectors meet in a
unique point. Because O is equally distant from the three vertices,
the circumscribed circle has its centre in O. Let us use this condition
to calculate the equation of the circumcentre:
OP2 = OQ2 = OR2
= d2
where d is the radius of the circumscribed circle. Using the
position vectors of each point we have:
(P - O)2 = (Q - O)2
= (R - O)2
The first equality yields:
P2 - 2 P · O + O2
= Q2 - 2
Q · O + O2
By simplifying and arranging the terms containing O on
the left
hand side:
2 ( Q - P ) · O = Q2
- P2
2 PQ · O = Q2 - P2
From the second equality we find an analogous result:
2 QR · O = R2 - Q2
Now we introduce the geometric product instead of the scalar product
in these equations:
PQ O + O PQ = Q2 - P2
QR O + O QR = R2 - Q2
By subtraction of the second equation multiplied by PQ
on the
right side minus the first equation multiplied by QR on the left,
we obtain:
PQ QR O - O PQ QR = PQ R2 - PQ Q2
- Q2QR + P2 QR
By using the permutative property on the left hand side and simplifying
the right hand side, we have:
PQ QR O - QR PQ O = P2 QR + Q2RP
+ R2 PQ
2 ( PQ ^ QR ) O = P2 QR
+ Q2 RP + R2 PQ
Finally, the multiplication by the inverse of the outer product
on the
left gives:
O = ( 2 PQ ^ QR ) -1 ( P2QR
+ Q2RP + R2 PQ )
= - ( P2QR + Q2RP
+ R2 PQ ) ( 2 PQ ^ QR ) -1
a useful formula for the calculation of the coordinates of the circumcentre.
For example, let us calculate the centre of the circle passing through
the points:
P = ( 2, 2 ) Q
= ( 3, 1 ) R = (
4, - 2 )
P2 = 8
Q2 = 10
R2 = 20
QR = R - Q = e1 - 3 e2
RP = P - R = - 2 e1 + 4 e2
PQ = Q - P = e1 - e2
PQ ^ QR = -2 e12 ( PQ ^ QR
) -1 = e12 / 2
O = - ( 8 ( e1 - 3 e2 ) +
10 ( - 2 e1 + 4 e2
) + 20 ( e1
- e2 ) ) e12 / 4
= - ( 8 e1 - 4 e2
) e12 / 4 = - e1 - 2 e2
= ( - 1, - 2 )
In order to deduce the radius of the circle, we take the vector
OP:
OP = P - O = P + ( P2 QR
+ Q2 RP + R2 PQ ) ( 2
PQ
^ QR ) -1
and extract the inverse of the triangle area as a common factor:
OP = ( 2 P PQ ^ QR + P2 QR
+ Q2 RP + R2 PQ ) ( 2
PQ
^ QR ) -1
= [ 2 P ( P ^ Q
+ Q ^ R + R ^
P ) + P2 QR
+ Q2 RP + R2 PQ ] ( 2
PQ
^ QR ) -1
= [ P ( P Q - Q P
+ Q R - R Q + R P - P R ) + P2
( R - Q ) + Q2 ( P - R )
+ R2 ( Q - P ) ]
( 2 PQ ^ QR
) -1
The simplification gives:
OP = ( P Q R - P R Q + P R P - P Q P
+ Q2 P - Q2 R + R2Q
- R2P ) ( 2 PQ ^ QR ) -1
= - (Q - P) (R -
Q)
(P - R) ( 2 PQ ^ QR ) -1 = - PQ
QR RP ( 2 PQ ^ QR ) -1
Analogously:
OQ = - QR RP PQ ( 2 PQ ^ QR ) -1
OR = - RP PQ QR ( 2 PQ ^ QR ) -1
The radius of the circumscribed circle is the length of any of these vectors:
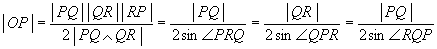
where we find the law of sines.
The addition of these vectors yields the
direction vector of the Euler line of the triangle:
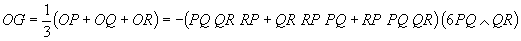
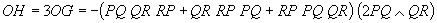
Updated: August 21st, 2010
 The
three bisectors of the sides of a triangle intersect in a unique point,
the circumcentre, which is the centre of the circumscribed circle. In order
to prove this statement we must only think that each point of the bisector
of the side PQ is equidistant from P and Q. Analogously
each point of the side PR is equidistant from P and R.
The intersection point O of both bisectors is simultaneously equidistant
from P, Q and R. Then
O also belongs to the
bisector of the side QR. Therefore the three bisectors meet in a
unique point. Because O is equally distant from the three vertices,
the circumscribed circle has its centre in O. Let us use this condition
to calculate the equation of the circumcentre:
The
three bisectors of the sides of a triangle intersect in a unique point,
the circumcentre, which is the centre of the circumscribed circle. In order
to prove this statement we must only think that each point of the bisector
of the side PQ is equidistant from P and Q. Analogously
each point of the side PR is equidistant from P and R.
The intersection point O of both bisectors is simultaneously equidistant
from P, Q and R. Then
O also belongs to the
bisector of the side QR. Therefore the three bisectors meet in a
unique point. Because O is equally distant from the three vertices,
the circumscribed circle has its centre in O. Let us use this condition
to calculate the equation of the circumcentre: