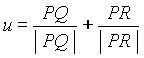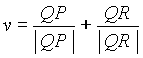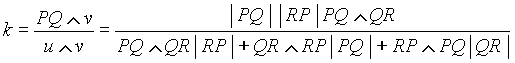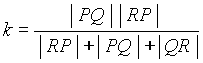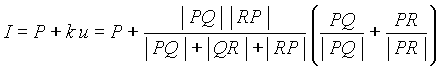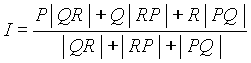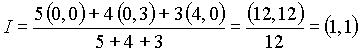Bisectrices
and incentre
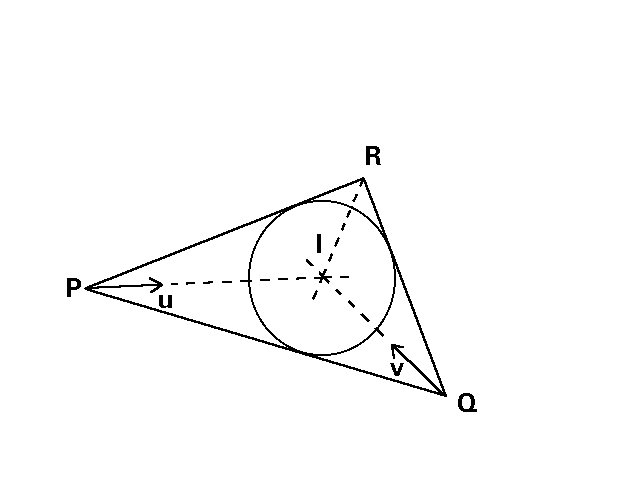 The three bisector lines of the inner angles of a triangle (the bisectrices)
intersect in a unique point, the incentre. Every point of the bisectrix
of the angle with vertex at P is equidistant from the sides PQ
and PR. Also every point of the bisectrix of Q is equidistant
from the sides QR and QP. Hence its intersection I
is simultaneously equidistant from the three sides, that is, I is
unique and it is the centre of the circle inscribed into the triangle.
In order to calculate the equation of a bisectrix, we take the sum of both
unitary vectors of adjacent sides:
The three bisector lines of the inner angles of a triangle (the bisectrices)
intersect in a unique point, the incentre. Every point of the bisectrix
of the angle with vertex at P is equidistant from the sides PQ
and PR. Also every point of the bisectrix of Q is equidistant
from the sides QR and QP. Hence its intersection I
is simultaneously equidistant from the three sides, that is, I is
unique and it is the centre of the circle inscribed into the triangle.
In order to calculate the equation of a bisectrix, we take the sum of both
unitary vectors of adjacent sides:
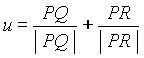
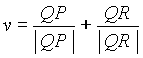
The incentre I is the intersection
of the bisectrix passing through P, whose directing vector is u,
and that passing through Q, with directing vector v:
I = P + k u
= Q + m v
k, m real
Arranging terms we find PQ
as a linear combination of u and v:
k u - m v = Q
- P = PQ
The coefficient k is:
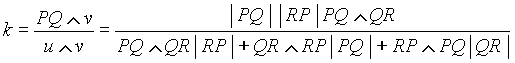
Since all outer products are equal
because they are twice the triangle area, this expression is simplified:
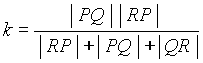
The centre of the inscribed circle
is:
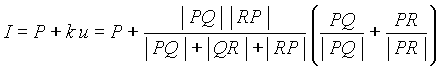
By taking common denominator and
simplifying, we arrive at:
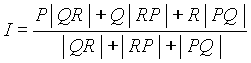
For example, let us calculate the
centre of the circle inscribed in the triangle with vertices:
P = ( 0, 0 )
Q = ( 0, 3 )
R = ( 4, 0 )
| PQ | = 3
| QR | = 5
| RP | = 4
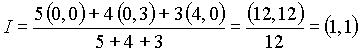
 The three bisector lines of the inner angles of a triangle (the bisectrices)
intersect in a unique point, the incentre. Every point of the bisectrix
of the angle with vertex at P is equidistant from the sides PQ
and PR. Also every point of the bisectrix of Q is equidistant
from the sides QR and QP. Hence its intersection I
is simultaneously equidistant from the three sides, that is, I is
unique and it is the centre of the circle inscribed into the triangle.
In order to calculate the equation of a bisectrix, we take the sum of both
unitary vectors of adjacent sides:
The three bisector lines of the inner angles of a triangle (the bisectrices)
intersect in a unique point, the incentre. Every point of the bisectrix
of the angle with vertex at P is equidistant from the sides PQ
and PR. Also every point of the bisectrix of Q is equidistant
from the sides QR and QP. Hence its intersection I
is simultaneously equidistant from the three sides, that is, I is
unique and it is the centre of the circle inscribed into the triangle.
In order to calculate the equation of a bisectrix, we take the sum of both
unitary vectors of adjacent sides: