MOVIMENT HARMÒNIC SIMPLE
 
Característiques fonamentals. Equació de l'elongació.
 

Per poder estudiar les característiques de les ones , és necessari que prèviament fem un estudi del moviment harmònic simple, moviment que es repetirà contínuament en les ones harmòniques, motiu pel qual haurem de dominar les seves característiques.

Diem que el moviment oscil·latori d'un cos és un moviment harmònic simple quan segueix una trajectòria recta i està sotmès a l'acció d'una força d'atracció proporcional al vector posició, amb origen al seu punt d'equilibri o centre d'oscil·lació, i de sentit contrari.

L'exemple més clar és el d'un cos sotmès a una força elàstica del tipus F= -Kx. Així podem considerar el moviment d'una cos subjectat a una molla elàstica, fixada per un extrem i que pot lliscar sense fregament sobre una superfície horitzontal, o bé el cas d'un cos subjectat d'una molla fixada al sostre i que per tant té un moviment vertical, com el cas del figura següent:

 

Si ens fixem bé en el moviment de la figura (imatge extreta de la baldufa ) podem anar deduint una sèrie de característiques:

1.- El moviment és periòdic.

2.- Es va succeint una posició de màxima separació de l'equilibri, (màxima elongació), amb un pas per la posició d'equilibri, seguit d'una màxima separació de l'equilibri però per la part negativa, nou pas per l'equilibri i finalment tornada a la màxima separació de l'equilibri.El seguit de totes aquestes posicions és el que anomenem cicle.

3.- La partícula es mou doncs entre un punt de valor màxim x=A i un valor mínim de x= -A. Mai trobarem la partícula per sobre de x=A ni per sota de x=-A

 

 
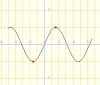
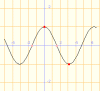
Per tal de trobar una funció que ens permeti calcular per qualsevol t quina és l'elongació de la partícula necessitarem una funció del tipus periòdic, com poden ser la funció sin x o bé cos x.

y = sin x

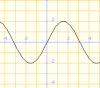
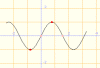
y = cos x

Aquestes funcions ens permeten trobar un valor màxim per l'elongació, un valor màxim negatiu, i un valor 0 que es repeteix dues vegades en cada període.En els casos representats, A=1 m, xo=0m i -A= -1. Si multipliquem la funció per una constant que simbolitzi l'amplitud màxima, diferent de1, podrem representar altres elongacions.

y= 2sinx

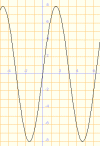
y=8sinx
Per altre banda observem que tant la funció sinx com cos x , tenen un cicle de 2. És a dir, per un període T en el qual la funció va de x=0 a x= 2 es succeeixen una sèrie de característiques que s'aniran repetint al llarg de tota la funció. Si canviem el valor de x ens variarà el valor d'aquest període
.

y=cos2x

y=sin2x

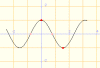
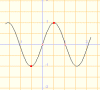
y=sin3x

si tal com indiquen les gràfiques, al variar x canvia el període, també canviarà la freqüència, definida com 1/T. Així, la funció que podrem considerar com a funció ideal per representar un m.h.s. serà del tipus:

on:

* A és el valor de l'amplitud (màxima elongació del moviment) en m

* s'anomena pulsació, i es relaciona amb el període segons l'equació :

Les unitats són rad/s

* és la fase inicial, és a dir l'angle, en rad, que haurem d'utilitzar per tal d'indicar la posició de x=0, per t=0 s

* és el que anomenem fase i les seves unitats són rad.

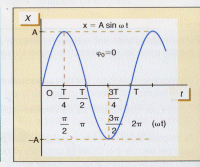
Podem observar que la funció serveix perfectament per descriure el moviment fixant-nos amb la taula i el gràfic següent:
t(s)

t (rad)
sin ( t)
x(m)
0
0
0
0
T/4
/2
+1
+A
T/2
0
0
3T/4
3/2
-1
-A
T
2
0
0
Gràfic i taula extrets de Física II, Batxillerat. Ed. EDEBÉ
 
Equació de la velocitat
 

Per obtenir l'equació de la velocitat per un m.h.s , caldrà derivar l'equació de la posició respecte del temps.

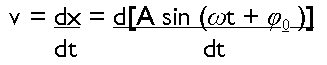
de forma que:

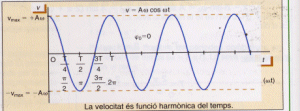
si observem el gràfic que correspon a la funció, podem deduir que:
t(s)

t (rad)
cos ( t)
v(m/s)
0
0
+1
+A
T/4
/2
0
0
T/2
-1
-A
3T/4
3/2
0
0
T
2
+1
+A
Gràfic i taula extrets de Física II, Batxillerat. Ed. EDEBÉ
 

* La gràfica de la velocitat està desfassada /2 respecte de la gràfica de l'elongació x.

* Quan x= A, la velocitat és nul·la,és a dir quan la partícula està situada en la màxima elongació, als extrems de la seva trajectòria.

* Quan x=0, la velocitat pren els seu valor màxim, v=A, cosa que passa quan la partícula és al centre de l'oscil·lació.
 
Equació de l'acceleració
 

si derivem l'equació de la velocitat respecte del temps podrem obtenir l'equació de l'acceleració

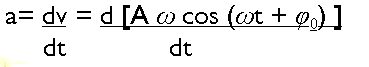
de forma que l'expressió de l'acceleració queda com:

i tenint en compte que , l'expressió anterior es pot escriure com:

Deduïm doncs que l'acceleració és directament proporcional a l'elongació i de sentit contrari,.

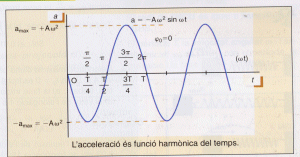
si observem la gràfica següent:
t(s)

t (rad)
sin ( t)
v(m/s)
0
0
0
0
T/4
/2
+1
-A
T/2
0
0
3T/4
3/2
-1
+A
T
2
0
0
Gràfic i taula extrets de Física II, Batxillerat. Ed. EDEBÉ
 

podem deduir que:

* La gràfica de l'acceleració esta desfasada en respecte de la gràfica de l'elongació.

* Quan x=A l'acceleració pren els seus valors màxims absoluts a= A, és adir quan la partícula està situada en els extrems de la seva trajectòria l'acceleració és màxima.

* Quan x=0 l'acceleració és nul·la. Per tant en el centre de l'oscil·lació no hi ha acceleració.
 
Comparació de la variació de l'elongació, velocitat i acceleració al llarg d'un període
 

Podríem resumir totes les conclusions en la figura1 si imaginem que la bola indica un objecte que es mou seguint un moviment harmònic simple sobre l'eix de les x.

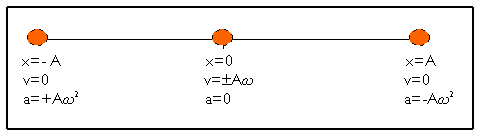Figura 1

Per altra banda, en la figura 2, podem veure com varia el vector velocitat al llarg d'un cicle. Si suposen que la bola parteix de x=0 per t=0, durant el primer quart de període la velocitat és positiva; en arribar a l'elongació màxima, donat que la velocitat pren el valor de 0 m/s, fa un canvi de sentit i la velocitat passa a ser negativa durant el segon i el tercer quart de període. Finalment, en l'últim quart perío, la velocitat torna ser negativa

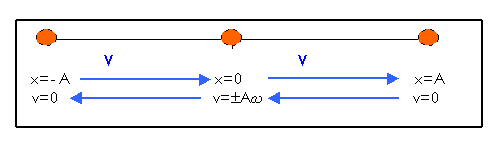Figura 2

Finalment, en la figura 3, veiem com canvia el vector acceleració, prenent un valor negatiu durant la primera meitat del període i un valor positiu en la segona meitat del període.

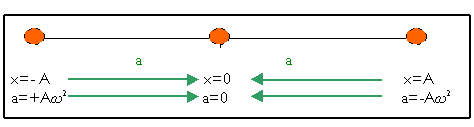Figura 3

si voleu veure com evoluciona l'elongació, la velocitat o l'acceleració en un m.h.s. cliqueu aquí