| Mòdul
3
|
Aplicacions
educatives de full de càlcul |
| Exercicis |
|
E31: Comparació econòmica Ara us proposem que analitzeu unes dades econòmiques d'Espanya corresponents al període 1977-1990. Les dades vénen expressades en pessetes. A partir de les dades de
les columnes A, B, C , D i E acabeu el full de càlcul calculant
els increments percentuals que figuren a les columnes F, G i H. Connecteu-hi
els dos gràfics, que ens relacionin els increments de l'IPC i de
l'SMI (Salari Mínim Interprofessional) i els increments dels preus
del litre de benzina i de la bombona de butà respectivament. Cal
tenir en compte que els increments es calculen sempre respecte als valors
de 1977. Per exemple, al 1985 el preu del butà va ser de 880 ptes.
Això implica el 276,07% d'increment sobre el preu del 1977, que
va ser de 234 ptes. Podria ser interessant que una vegada fet tot això
canviéssiu algunes dades de 1990, i així observar els canvis
gràficament.
|
|
|
|
E32: Demografia En aquest exercici us proposem que estudieu la variació de la població de quatre ciutats. El full de càlcul que heu de dissenyar ha de ser semblant a:
Fixeu-vos com en la fila 3 teniu les poblacions inicials, que surten repetides a la fila corresponent a l'any 2002. En la fila 4, heu de situar els percentatges de creixement anual, és a dir, el tant per cent que creix la població de cada ciutat cada any, respecte l'any anterior. Fixeu-vos també com la ciutat D té un creixement negatiu. Això significa que aquesta ciutat perd, cada any, el percentatge de població que està indicat en la cel·la E4. En el rang B7:E15, heu d'entrar les fórmules necessàries per aconseguir els resultats que es poden observar. També heu de dissenyar un gràfic, on es representin aquestes dades, similar a:
|
|
| E33: Llei de Boyle-Mariotte La llei de Boyle-Mariotte diu que el volum ocupat per una mateixa massa gasosa, a temperatura constant, és inversament proporcional a la pressió que suporta. És a dir, si P és la pressió i V el volum, seria: P V = constantAixò és, un gas a pressió P i a volum V, si passa a pressió P' el seu volum serà V', de tal manera que es complirà: P V = P' V' = constantO si el gas de pressió P i volum V varia el volum a V'' aleshores, la seva pressió variarà a P'', de manera que: P V = P' V' = P'' V'' = constantLa pressió s'acostuma a mesurar en mil·límetres de mercuri (mm Hg) i el volum en centímetres cúbics (cc). Així, per exemple, un gas que ocupa 76,8 cc a la pressió de 772 mm de hg, el volum que ocuparà a 1 atmosfera de pressió (1 atm = 760 mm de hg) serà: (76,8 cc) x (772 mm de hg) = V x (760 mm de hg)És a dir, |
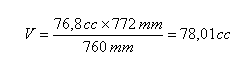
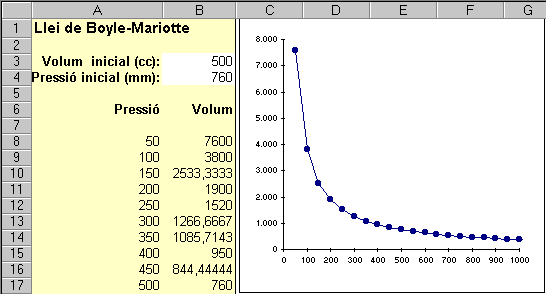
En resum, si es manté la temperatura constant, en variar la pressió, el volum varia seguint la llei de Boyle-Mariotte. Es proposa construir un full de càlcul tal que, donats un volum i una pressió inicials, trobi el volum corresponent a una pressió variable segons un increment (de 50 en 50 mm) i a partir d'un primer valor (50 mm). Aquest full ha de poder simular les diverses situacions en variar els valors de les cel·les B3 i B4. Construïu la gràfica associada. Aquest full podria ser:
|
|
|
|
A partir de les dades oficials de matrícula d'ESO del curs 2001-02, heu d'elaborar un full de càlcul amb uns gràfics com es veuen a la figura:
|
|
|
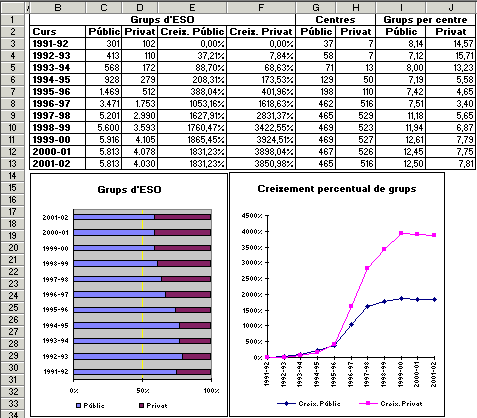
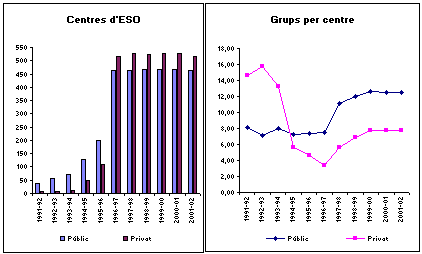
E35: L'Ensenyament secundari obligatori a Catalunya (II) A partir de les dades publicades
pel Departament d'Ensenyament de la Generalitat de Catalunya, sobre la
implantació de l'ESO en els darrers anys, es poden fer diferents
gràfics comparatius. Fixeu-vos en la figura següent:
|
  |
|
Es proposa que feu un full de càlcul semblant amb els gràfics associats. Cal tenir en compte que:
|
|
E36: L'Ensenyament secundari obligatori a Catalunya (III) A continuació us presentem més dades sobre el mateix tema, recollides de http://www.gencat.es/ense/depart/pdf/esta0102/series/series7.pdf
En aquest exercici us proposem que dissenyeu un full de càlcul amb gràfics associats per tal de: Per resoldre correctament aquest exercici, haureu de tenir en compte les dades i els tipus de gràfics fets servir en l'exercici anterior.Aneu provant diferents tipus
de gràfics i trieu aquells que expliquin millor aquests resultats.
|