Fig.3.1. El THEMANCUBUSKIE

El primer pas de la nostra recerca geomètrica cap a la quarta dimensió va consistir en agrupar les figures més comunes per nosaltres (triangle, cub,...) en famílies. Aquestes famílies foren:

1. la cubus: punt, línia, paral.lelograms i prismes amb angles rectes.
2. la tetrahedron: punt, línia, triangles i tetràedres.
3. la spherae: punt, línia, cercles (amb cons plans) i esferes (amb cons amb relleu)

La hipòtesi de la qual partim és la que diu que una figura en una dimensió està formada per la figura homòloga de la dimensió anterior que s'ha desdoblat, és a dir, que s'ha doblat i la clonació ha gosat fugir de la dimensió que l'empresonava, situant-se paral.lelament a l'interior, i interaccionant-se a l'original formant la figura en la dimensió següent.

Per a explicar el procediment del cub, partim d'un aventurer punt que decideix fer un apassionant viatge a través de les dimensions. Aquest punt l'anomenem El Gran Patriarca, perquè a partir d'ell s'originen totes les figures ja que en dimensió zero no pot existir cap altra figura, o el que seria el mateix, totes les figures empresonades a la dimensió zero són iguals.

A la dimensió zero tenim El Gran Patriarca, o millor dit, només podem veure un sol punt. Aquest punt es duplica; el nou nat l'estirem cap a qualsevol direcció de l'espai. Unint aquests dos punts amb una recta. Així entrem en la dimensió de les rectes, la primera dimensió.

La recta conserva una part de l'atreviment del punt original, i crea una recta idèntica a ella mateixa pel procediment abans esmentat, és a dir, el de clonació i separació. Aquesta recta l'estirem de manera que quedi paral.lela a la primera recta, i que les rectes que també uneixen els vèrtexs situats als extrems d'aquestes siguin paral.leles i també ortogonals, i de la mateixa longitud que la recta que prové de la primera dimensió. Cal unir única i exclusivament els vèrtexs homòlegs, els que provenen del mateix vèrtex (de la recta original), per tal de construir la figura convenient. Així obtenim un quadrat, que habita originàriament en la segona dimensió.

I continuant amb la seva odissea, el quadrat decideix crear un quadrat idèntic a ell que, es desplaça deixant una estela de longitud igual a la de la recta de la primera dimensió. Cal dir que les arestes de l'estela són paral.leles entre elles i que cadascuna és perpendicular a les rectes que formen el quadrat original. I tenim l'indígena en les tres dimensions: el cub.

I si una línea està formada per punts, un quadrat per rectes i un cub per quadrats, ¿no seria lògic que la figura relativa al cub en quatre dimensions, que nosaltres anomenem THEMANCUBUSKIE, no estigués formada per cubs?. La nostra criatura tetradimensional és una figura amb cubs per cares. La forma d'aconseguir aquesta figura és la següent: a partir del cub que tenim, en clonem un al costat idèntic a l'anterior. Ara tenim dos cubs, i els seus vèrtexs els unim amb arestes i ens queda el nostre simpàtic descobriment.

Ara veurem tot el procés evolutiu del punt fins al THEMANCUBUSKIE:

Fig.3.3. La línia és la primera dimensió

Fig.3.4. El quadrat ja és perceptible en la segona dimensió

Fig.3.5. El cub és el quadrat en tres dimensions

Fig.3.6. El THEMANCUBUSKIE és el cub en quatre dimensions

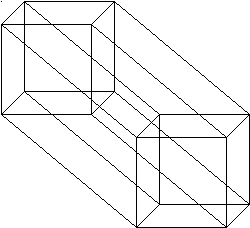
Aquesta figura té, com en tres dimensions, diferents perspectives. Així que també hem estudiat altres perspectives com per exemple la que segueix:

Fig.3.7 El THEMANCUBUSKIE aquesta n'és una altra

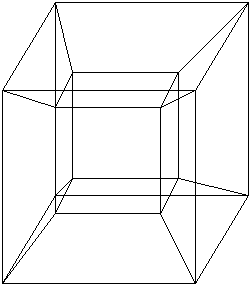
Ara ens dedicarem a analitzar la nostra creació numèricament:

Aquest és el quadre que a partir de les nostres observacions ens permetrà escriure la Llei Universal de la Família del Quadrat.

En aquest quadre es mostra una curiosa relació: una casella multiplicada per dos i sumada a la que es troba sobre seu és igual al valor de la casella del costat de la primera.

Explicació d'aquesta curiosa llei universal:

Els vèrtexs de dimensió en dimensió van creixent en progressió geomètrica de r = 2 perquè la figura es duplica i sempre és constant. Així la nostra simpàtica criatura té setze vèrtexs. Aquest valor prové del càlcul següent: t_n = t₁.r^n-1, on t és el terme i n és el número de terme, que en aquest cas coincideix amb la dimensió.

Per tant, a la quarta dimensió el nombre de vèrtex és de 16. Ara, amb el senzill càlcul proposat abans de la casella de sota multiplicada per dos més la de dalt, sabrem quantes arestes té un THEMANCUBUSKIE. Així:

Així el THEMANCUBUSKIE té 32 arestes.

Pel mateix càlcul podem saber quantes cares, cubs i THEMANCUBUSKIES. Així, 24 cares, 8 cubs i 1 THEMANCUBUSKIE té la figura tetradimensional.

Així, successivament en tots els càlculs que es vulguin fer per esbrinar quantes arestes, per exemple, tindria la figura de la família del quadrat en 30.000 dimensions.