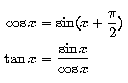Quan vam començar a realitzar el programa informàtic vàrem intentar veure quin tipus de funcions podien intervenir a l'hora de expressar un camp o una força. Una de les funcions bàsiques que necessitàvem per fer el nostre treball era el sinus, funció trigonomètrica que no existia en el llenguatge de programació que vàrem utilitzar. Llavors, el problema que se'ns va plantejar era trobar un mètode, per poder fer els càlculs del sinus el màxim de precisos possible. Vàrem començar una investigació dels diferents tipus de sistemes que ens podrien servir per fer un bon càlcul. Així primer de tot utilitzàrem el mètode d'aproximació pels polinomis de Lagrange que, en el primer moment ens va semblar que era suficientment precís. Però un cop entrats en els càlculs del moviment de la partícula vàrem veure que el mètode utilitzat no era prou precís i ens produia error. Així doncs, buscàrem un altre procés pel qual els errors que ens donaven fins aquell moment no es produïssin. Aquest fou que fou el de buscar un polinomi que s'aproximés el màxim a la zona de 0 a
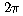de la gràfica del sinus. Ara a continuació desenvoluparem pas a pas
cadascun dels mètodes anteriorment comentats.
- Càlcul mitjançant els polinomis de Lagrange.
Primer de tot cal destacar que la gràfica del sinus és periòdica la qual cosa ens permetrà simplificar els càlculs. Sabent que la gràfica de 0 a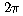 es repeteix
simètricament vàrem aplicar el mètode de Lagrange en aquest
segment de funció i la resta de valors els vàrem extreure a
partir de la idea de periodicitat de la gràfica. Així calcular
el sinus de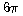 
és el mateix que
calcular el de 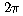que és el mateix
que calcular el de 0.
Agafem l'intèrval de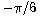
a
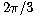i el dividim en 6 subintervals.
Llavors segons el mètode de Lagrange agafem tres punts, dintre
dels quals hi hagi el valor de sinus que volem calcular. En
aquest espai el polinomi de Lagrange ens farà el càlcul del
sinus. El mètode de Lagrange comença amb una taula de valors de
la zona que ens interessa:
:
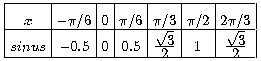
El primer pas és calcular els sis polinomis de Lagrange corresponents a la distribució de punts que hi ha a la taula: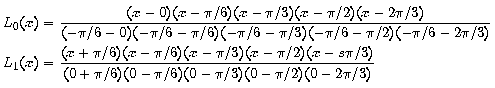
.
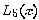Un cop tenim tots els polinomis podem escriure el polinomi final.
Quan introduïm el primer valor de x de la taula en el
polinomi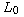 
el resultat és 1. En
canvi quan introduïm els altres valors de la taula el resultat
del polinomi és 0. Pel segon polinomi el valor que fa que el
resultat sigui 1 és el segon, pel tercer el tercer i així
successivament. Així veiem que l'únic polinomi que passarà pel
punt que ens interessa serà el que no resulti 0. Ara podem
extreure el polinomi interpolador, que és el polinomi que ens
donarà el resultat del sinus que ens interessa i que, a la
vegada, és l'únic polinomi que passa pels sis punts de la taula.
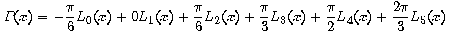
- Aproximació pel polinomi d'onzè grau.
Per tal de millorar el càlcul del sinus vàrem buscar un funció la gràfica de la qual fos molt semblant a la del sinus, com a mínim a la zona simètrica del sinus. I en les nostres investigacions trobàrem que el polinomi de grau 11 era quasi perfectament igual a la gràfica del sinus de -
a .
Per tal de trobar la fórmula general d'aquest polinomi vàrem
començar amb polinomis més petits, i posteriorment ho vàrem
aplicar al polinomi de grau 11. Exactament ho férem pel polinomi
de grau 7:
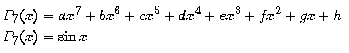
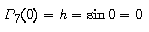
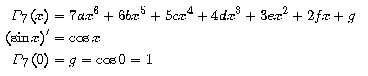
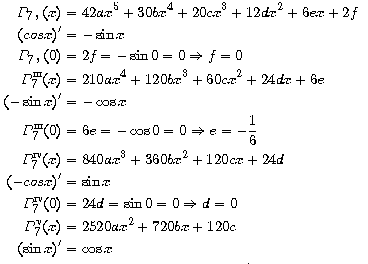
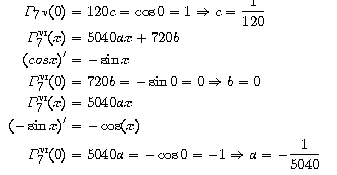
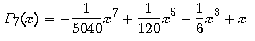
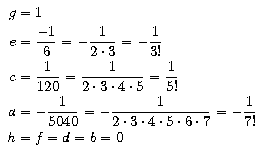
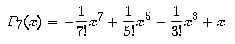
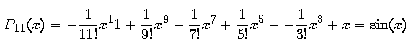
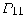iguala a
sin x al punt 0 i a les seves onze primeres derivades.
El càlcul de la tangent i el cosinus és molt fàcil d'obtenir un cop es té el sinus. Per simples raons trigonomètriques obtenim aquest dos càlculs:
