CAMPS.EXE. Un cop ha acabat l'entrenyable melodia i de
l'increïble presentació, apareixerà una pantalla on s'hi han
d'introduir totes les dades:
- Posició de la partícula en l'eix de les "x",
- posició de la partícula en l'eix de les "y",
- velocitat en l'eix de les "x",
- velocitat en l'eix de les "y",
- massa,
- força a l'eix de les "x",
- força a l'eix de les "y",
- fórmula de l'Energia Potencial,
- diferencial de temps,
- separació entre unitats,
- escala de la pantalla (unitats per píxel),
Si el que es vol introduir és l'energia potencial llavors el que cal fer és deixar en blanc les forces. Igualment, si es vol que faci els càlculs a partir de les forces és recomanat que es deixi en blanc l'energia potencial.
Un altre fet destacat és que a la zona central de la pantalla apareix una altra representació gràfica que correspon a les velocitats, aquesta representació correspon a les velocitats de la partícula en cada punt. Deixant per suposat que estan a la mateixa escala, tant les posicions com les velocitats.
Per sortir del programa heu de prémer la tecla
ESC i respondre
S.
- Moviment d'un planeta degut a un camp
gravitatori. Aquest va ser el cas que ens va fer concloure que
la partícula perdia energia. Introduïu les següents dades en la
pantalla:
- Posició de la partícula en l'eix de les "x":
15, - posició de la partícula en l'eix de les "y":
-15, - velocitat en l'eix de les "x":
25, - velocitat en l'eix de les "y":
25, - massa:
1, - força a l'eix de les "x": (en blanc),
- força a l'eix de les "y": (en blanc),
- fórmula de l'Energia Potencial:
-51000/((x^2+y^2)^(1/2)), - diferencial de temps:
0.002, - separació entre unitats:
100, - escala de la pantalla (unitats per píxel):
0.1,
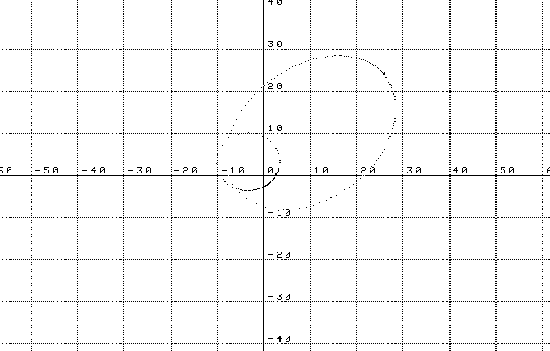
Fig.4.1. Moviment orbital - Posició de la partícula en l'eix de les "x":
- Caiguda lliure d'un cos:
- Posició de la partícula en l'eix de les "x":
25, - posició de la partícula en l'eix de les "y":
25, - velocitat en l'eix de les "x":
15, - velocitat en l'eix de les "y":
15, - massa:
1, - força a l'eix de les "x":
0, - força a l'eix de les "y":
-9.8, - fórmula de l'Energia Potencial: (en blanc),
- diferencial de temps:
0.002, - separació entre unitats:
100, - escala de la pantalla (unitats per píxel):
0.1,

Fig.4.2. Caiguda lliure - Posició de la partícula en l'eix de les "x":
- Moviment causat per la interacció d'un punt de
càrrega negativa i un electró en moviment (repulsió):
- Posició de la partícula en l'eix de les "x":
50, - posició de la partícula en l'eix de les "y":
50, - velocitat en l'eix de les "x":
-30, - velocitat en l'eix de les "y":
-30, - massa:
1, - força a l'eix de les "x": (en blanc),
- força a l'eix de les "y": (en blanc),
- fórmula de l'Energia Potencial:
51000/((x^2+y^2)^(1/2)), - diferencial de temps:
0.002, - separació entre unitats:
100, - escala de la pantalla (unitats per píxel):
0.1,
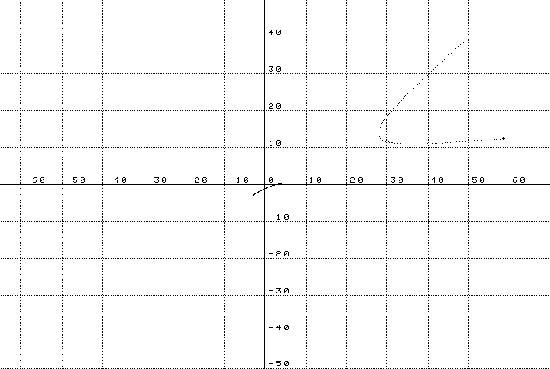
Fig.4.3. Repulsió - Posició de la partícula en l'eix de les "x":
- Moviment vibratori harmònic:
- Posició de la partícula en l'eix de les "x":
10, - posició de la partícula en l'eix de les "y":
10, - velocitat en l'eix de les "x":
10, - velocitat en l'eix de les "y":
10, - massa:
1, - força a l'eix de les "x":
-50x, - força a l'eix de les "y":
0, - fórmula de l'Energia Potencial: (en blanc),
- diferencial de temps:
0.002, - separació entre unitats:
100, - escala de la pantalla (unitats per píxel):
0.1,
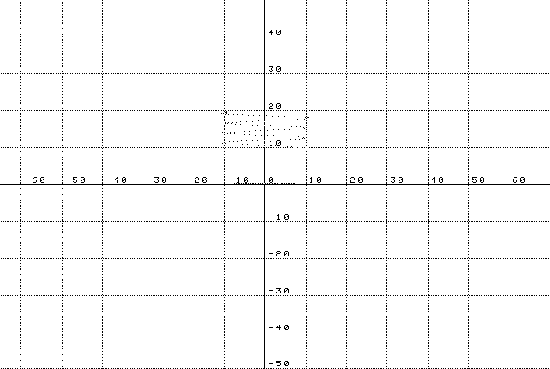
Fig.4.4. Moviment vibratori harmònic - Posició de la partícula en l'eix de les "x":