Definició
- Una corba qualsevol a l'espai està
definida per dues equacions qualsevol en la forma:
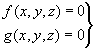 .
.
En el nostre cas limitarem a que les dues equacions anteriors només puguin tenir expressions lineals i quadràtiques, això és, les variables només poden presentar potències de primer o de segon grau.
Amb la restricció anterior podem tenir els següents:
Exemples
- Circumferència.
Geomètricament, una circumferència es defineix com el lloc geomètric dels punts d'un pla que equidisten d'un punt fix d'aquest pla, anomenat centre.
Des del punt de vista algebràic,
l ’equació d’una circumferència a l’espai centrada a l’origen
de coordenades i que està sobre el pla coordenat XY és:
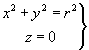 ,
on r és el radi de la circumferència.
,
on r és el radi de la circumferència.
En aquest material, per poder situar una circumferència en l'espai ho farem donant el seu centre, el seu radi i un vector normal al pla en que està situada la circumferència.
Exercici 1: Obre la , dibuixa els eixos de coordenades i prova d'imaginar-te com serà una circumferència de centre C=(3,3,0), vector normal (0,1,0) i radi 2. Després, dibuixa-la. .
-
L'el·lipse és el lloc geomètric dels punts d'un pla tals que la suma de distàncies a dos punts fixos del mateix pla, anomenats focus, és constant.
Algebràicament, l’equació d’una el·lipse a l’espai centrada a l’origen de coordenades i que està sobre el pla coordenat XY és:
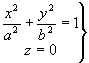 ,
on a i b són les distàncies des del centre
fins als punts més llunyans i pròxims de l’el·lipse.
,
on a i b són les distàncies des del centre
fins als punts més llunyans i pròxims de l’el·lipse.Ací, definirem l'el·lipse donant el seu centre i dos vectors que van des del centre fins, un al punt més llunyà, i l'altre, al punt més proper. De fet, aquests vectors es corresponen amb els semieixos principal (o major) i secundari (o menor) de l'el·lipse.
L'el·lipse verifca l'anomenada relació fonamental de l'el·lipse: c2=a2+b2, on c és la posició dels focus (punts (c,0,0) i (-c,0,0)).
Podem veure l'el·lipse i els seus elements en la figura següent:
Exercici 2 : Utilitza la per dibuixar una el·lipse de centre C=(2,0,4), vector del radi major (3,0,3) i vector del radi menor (1,0,-1). .
La paràbola és el lloc geomètric dels punts d'un pla que estan a la mateixa distància d'un punt fix, anomenat focus, i d'una recta fixa, anomenada directriu, situats els dos en el mateix pla.
L’equació de la paràbola situada en el pla XY amb el vèrtex en l'origen de coordenades i que té el focus en el punt (p/2,0,0) i la directriu paral·lela a l'eix Y i que passa pel punt (-p/2,0,0) és:
, on p és la distància des del focus fins la directriu.
En la miniaplicació, definirem una paràbola donant les coordenades del focus i el punt i el vector director de la directriu. Podem veure un exemple amb tots els seus elements en la representació següent:
Exercici 3 : Utilitza la per dibuixar una paràbola de focus F=(0,-3,0), i directriu de punt P=(0,3,0) i vector (1,0,0). .
La hipèrbola és defineix com el lloc geomètric dels punts d'un pla tals que el valor absolut de la diferència de les seves distàncies a dos punts fixos del mateix pla, anomenats focus, és constant.
L’equació de la hipèrbola situada en el pla XY amb focus sobre l'eix X en els punts (c,0,0) i (-c,0,0) és:
, on com s'ha dit c ens dóna la posició dels focus, a determina el punt de tall de la hipèrbola amb l'eix X (punts: (a,0,0) i (-a,0,0)) i b ve donat per la relació fonamental de la hipèrbola c2=a2+b2.
En el nostre cas, definirem una hipèrbola donant les coordenades del centre de la hipèrbola i dos vectors perpendiculars: un en la direcció de l'eix de la hipèrbola (recta que passa pels dos focus) i tal que el seu mòdul ens dóna el paràmetre a; i l'altre, que ens acaba de definir el pla que conté la hipèrbola i de forma que el seu mòdul ens dóna el paràmetre b. Veiem un exemple amb aquests elements en la representació següent:
Exercici 4 : Utilitza la per dibuixar una hipèrbola de centre C=(0,0,0) i vectors (0,0,3) i (4,0,0). .