
|
Les funcions trigonomètriques
Les funcions trigonomètriques serveixen com a model per expressar matemàticament les característiques de les ones sonores. És per això que anem a fer un petit estudi de les seves propietats. Comencem per la més simple: La funció $f(x)=\sin(x)$ té la representació gràfica següent: 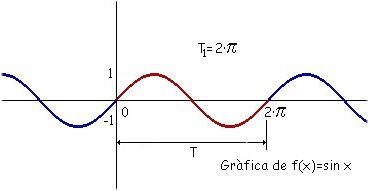 La gràfica de la funció es repeteix en incrementar o disminuir el valor de $x$. A partir de la que es troba a l'interval $[0,2\pi ]$, es podria generar tota la resta. Aquest fenomen s'esdevindrà a les ones sonores. Això es degut a la propietat següent: $\sin(x)=\sin(2\pi+x)$ , per qualsevol angle $x$. Diem que la funció $f(x)=\sin(x)$ és una funció periòdica de període $2\pi$. Això el que ve a dir és que l'ona es repetirà cada $2\pi$. 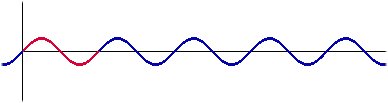 Però, què passarà si augmentem el valor que multiplica la $x$? Prenem, per exemple, la funció $f(x)=\sin(2x)$
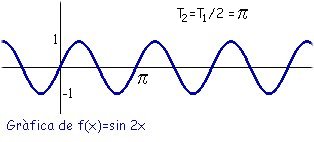
En aquest cas, el període és la meitat del de la funció anterior, és a dir $\pi$. De 0 a $\pi$ hi ha una oscil·lació completa. Físicament, diem que la seva freqüència és doble que l'anterior. Si, en canvi, multipliquem sin x per un número qualsevol observarem que la funció experimenta uns canvis diferents. Considerem la funció $f(x)=3\cdot \sin(x)$: 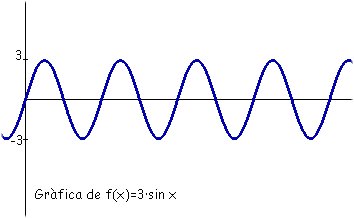 Gràficament, ha patit una deformació. Hi ha hagut un estirament en direcció vertical. El període continua sent el mateix que el de la funció $f(x)=\sin(x)$, és a dir, l'ona continua tenint la mateixa longitud però podem veure que ha augmentat la seva amplitud d'ona (A). En el llenguatge musical diem que ha augmentat la seva intensitat. Vegem què passa quan sumem dues funcions del tipus $f(x)=\sin(n\cdot x)$ com $f(x)=\sin(x)+\sin(2x)$ 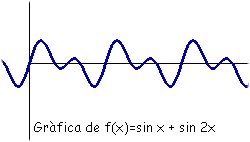 La funció continua tenint el mateix període ($2\pi$) però la forma de l'ona ha canviat. Observació: Les funcions del tipus $f(x)=\sin(n\cdot x)$, on $n$ sigui un número natural, com les que hem vist anteriorment sempre tindran com a període $\frac{2\pi}{n}$. D'aquest fet deduïm la següent taula:
Si volem expresar una funció trigonomètrica de període $T$, aquesta vindrà donada per l'expresió: $f(x)=\sin \left(\frac{2\pi}{T}\cdot x\right)$, o bé fent servir el fet que la freqüència $\nu=\frac{1}{T}$, l'expressió es transforma en: $g(x)=\sin \left(2\pi}\cdot \nu\cdot x)$ Igualment, amb les funcions del tipus $f(x)=\sin(n\cdot x)+\sin(m\cdot x)$, el període serà $\frac{2\pi}{MCD(n,m)}$. Exemple: $f(x)=\sin(x)+\sin(2\cdot x)+\sin(3\cdot x)$ Sabent que el MCD de {1, 2, 3} és 1, podem deduir que el seu període serà $2\pi}$. Per tant, si en una funció del tipus $f(x)=\sin(n\cdot x)$ li sumem funcions del tipus $f(x)=\sin(k\cdot n\cdot x)$ el període (i, per tant, la freqüència) continua sent el mateix. Exemple: $f(x)=\sin(4x)+\sin(6x)$. Sabent que el MCD de {4, 6} és 2, podem deduir que el seu període serà $\frac{2\pi}{2}=\pi$. Com es pot veure a la construció feta amb el programa GeoGebra. Gràfica de $f(x)=\sin(4x)+\sin(6x)$
De la mateixa forma, si a una funció del tipus $f(x)=\sin(n\cdot x)$ li sumem funcions del tipus $f(x)=\sin(k\cdot n\cdot x)$ amb amplitud cada cop més petita ens apareixeran models d'ones semblants a les produïdes pels instruments musicals. Aquests múltiples que se li sumen a l'ona primària reben el nom d'harmònics.
Cada so instrumental tindrà una forma d'ona determinada degut a la varietat dels harmònics que se li han afegit a l'ona principal, el que ens permetrà reconèixer de quin instrument procedeix. A música, aquest fenomen rep el nom de timbre.
|
