Àlgebra

1.9 Matemàtica financera

Els diners es compren i es venen. El preu del diner no coincideix amb el seu valor, sinó que resulta d’afegir al valor una quantitat variable que s’anomena interès.
L’interès s’estableix i es paga amb relació a un període de temps que acostuma a ser l’any. L’interès anual per unitat s’anomena taxa d’interès.

Si al final d’aquest període els interessos se separen del capital i aquest continua produint es parla d’interès simple.
Les quantitats de diners a interès simple formen una progressió aritmètica que té per diferència la taxa d’interès i. Per tant

on C₀ és el capital inicial, C_n el capital després de n períodes, i n el nombre de períodes.

Quan els interessos no se separen del capital i també es deixen a produir durant un altre període es parla d’interès compost.
Les quantitats de diners a interès compost formen una progressió geomètrica que té per raó 1+i, on i és la taxa d’interès. Per tant

Sovint els interessos no s’acumulen cada any sinó en períodes més curts, k vegades l’any. Llavors en cada període es paga un interès  . A final de l’any l’interès que això representa no és i (interès nominal), sinó un valor que s’anomena TAE o taxa anual equivalent.
La relació entre tots dos és:  1 + TAE = 

S’anomena renda al pagament periòdic d’una quantitat determinada. Són exemples: els plans de pensions, les assegurances, la devolució d’un prèstec o les vendes a terminis.
Quan el capital no està disponible fins al final de la renda es parla d’una operació de capitalització. Si la renda es paga al principi del període és una capitalització avançada; si es paga al final, és una capitalització retardada.

El capital obtingut per una capitalització retardada és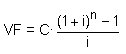 
i per una capitalització avançada 
on  VF: valor final del capital,  i: taxa d’interès, n: nombre de períodes,  C: valor de cada pagament (quota)

Quan el capital està disponible al principi de la renda es parla d’una operació d’amortització.
Llavors si VA és el valor actual del capital es té: